Coordinate bug
A bug of negligible size starts at the origin of the coordinate plane. First, it moves 1 unit right to ( 1 , 0 ) . Then it makes a 9 0 ∘ turn counterclockwise and travels 2 1 a unit to ( 1 , 2 1 ) . If it continues in this fashion endlessly, each time making a 9 0 ∘ turn counterclockwise and traveling half as far as in the previous move, to which of the following points will it come closest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Separating x and y is great. It can be extended to a 3D bug in xyz. Complex numbers won't work here!
Say the bug lives in the complex plane, and its path is z 0 , z 1 , z 2 , … . We have z 0 = 0 and z n + 1 = z n + 2 n 1 e i n 2 π
which looks ghastly, but encodes both the bug's turning (in the e i n 2 π term) and the path shortening (in the 2 n 1 term). This means we can find the bug's ultimate destination - z ∞ - by summing a geometric series: z ∞ = n = 0 ∑ ∞ 2 n 1 e i n 2 π = 1 − 2 1 e i 2 π 1 = 5 4 + 5 2 i
I am in grade 9 and have not started complex numbers yet. But I am happy to see this problem being solved with complex numbers.
Maybe it's a complex bug.
Convert the x y -plane into the complex plane of z , where the real part ℜ ( z ) = x and imaginary part ℑ ( z ) = y . Let the first move be u 0 = 1 , the second move be u 1 = 2 i , third move be u 2 = − 4 1 and so on. Then the final position of the bug after n th move is given by z n = u 0 + u 1 + u 2 + ⋯ + u n − 1 . We note that a turning of 9 0 ∘ anticlockwise in a complex plane is equivalent to multiplied by i , the imaginary unit . Then we have:
z n ⟹ n → ∞ lim z n = k = 0 ∑ n − 1 u k = k = 0 ∑ n − 1 ( 2 i ) k = k = 0 ∑ ∞ ( 2 i ) k = 1 − 2 i 1 = 2 − i 2 = 5 2 ( 2 + i ) = 5 4 + 5 2 i
Therefore, the final coordinate of the bug is ( 5 4 , 5 2 ) .
Since there are already multiple solution utilizing complex numbers, I'll give a solution using linear algebra.
Let's denote the first move by the vector b = [ 1 0 ] .
Now counterclockwise rotation of 9 0 degrees corresponds to multiplying by the matrix M = [ 0 1 − 1 0 ] ,
and halving the length corresponds to multiplying by the matrix
N = [ 2 1 0 0 2 1 ] .
Let's denote their product by N M = A = [ 0 2 1 − 2 1 0 ] .
Now we can get the next vector to add by multiplying the previously added vector by matrix A .
Continuing this indefinitely we see that the sum x = k = 0 ∑ ∞ A k b gives the limit point if it converges.
Since the eigenvalues of the matrix A , which are ± 2 i , have absolute values less than 1 , the geometric series k = 0 ∑ ∞ A k converges towards ( I − A ) − 1 and thus
x = ( I − A ) − 1 b = ( [ 1 0 0 1 ] − [ 0 2 1 − 2 1 0 ] ) − 1 [ 1 0 ] = [ 1 − 2 1 2 1 1 ] − 1 [ 1 0 ] = [ 5 4 5 2 − 5 2 5 4 ] [ 1 0 ] = [ 5 4 5 2 ] .
Thus the limit point is ( 5 4 , 5 2 ) .
Why are you guys using so strange methods to solve this?? Maybe that's not really strange but for me it's like Greek and Latin.
A good way to think of this problem is to find the x and y co-ordinates separately.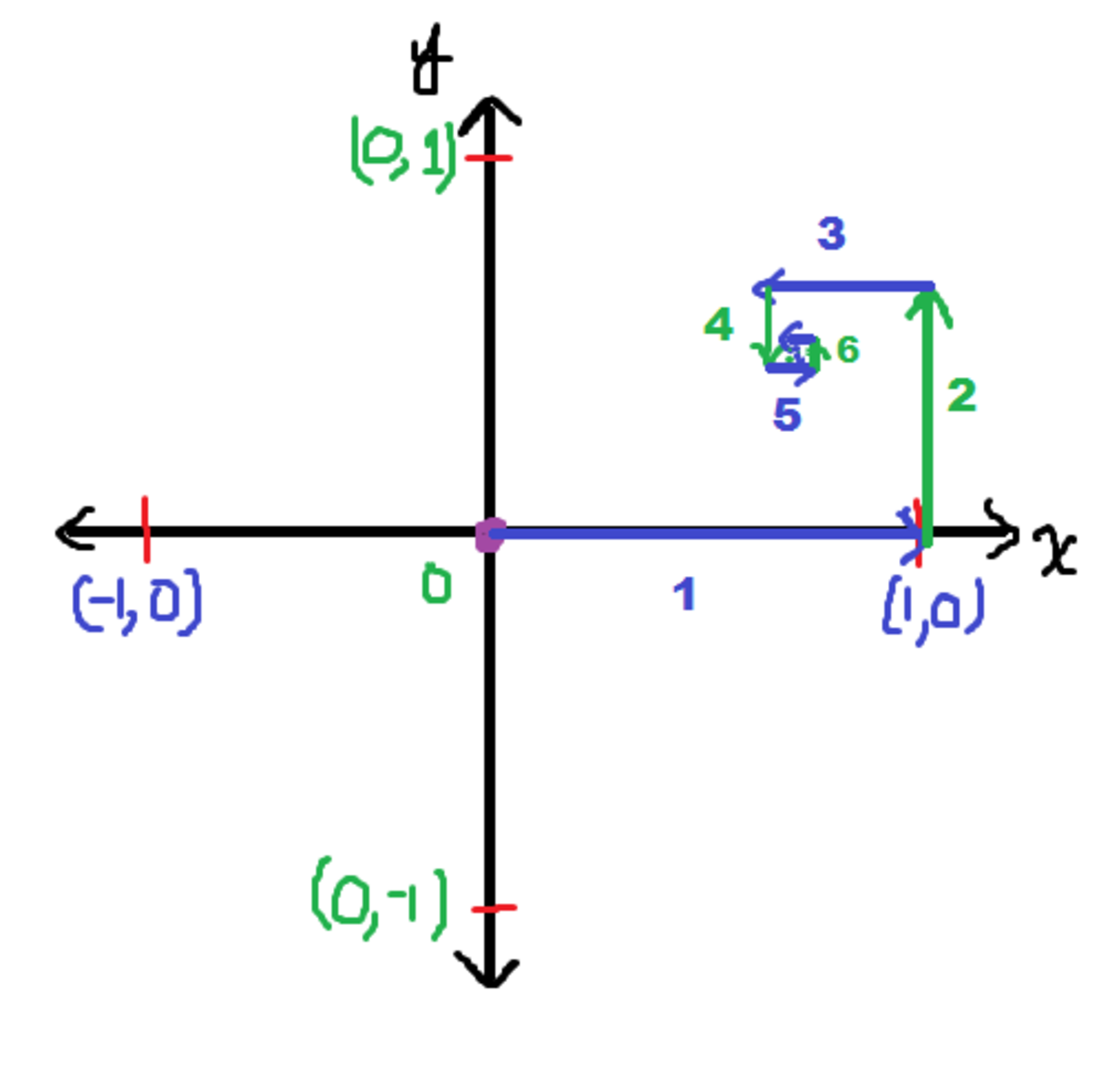
Look at the diagram,
Along the x axis:
If we take a move rightward as positive and the move leftward as negative , then the bug takes the following moves:
1 , 4 − 1 , 1 6 1 , 6 4 − 1 . . . ∞
Notice that it forms an infinite geometric series with common ratio(r) = 4 − 1
Where the bug lands can be thought of as the sum of this infinite geometric series:
S u m = 1 − r a
⇒ S u m = 1 − 4 − 1 1 = 5 4
This gives us the x coordinate.
Along the y axis:
If we take a move upward as positive and the move downward as negative , then the bug takes the following moves:
2 1 , 8 − 1 , 3 2 1 , 1 2 8 − 1 . . . ∞
Notice again that it forms an infinite geometric series with common ratio(r) = 4 − 1
Again, where the bug lands can be thought of as the sum of this infinite geometric series:
S u m = 1 − r a
⇒ S u m = 1 − 4 − 1 2 1 = 5 2
This gives us the y coordinate.
So, the point where it approaches is ( 5 4 , 5 2 )