Coordinate Challenge
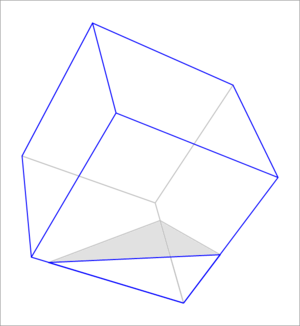
A cube with an edge length of units, is partially immersed in water whose surface coincides with the plane. Its edges meeting at the lowest point of the cube, intersect the water surface at , , . Determine the coordinates of the cube vertex that is highest above the water surface (that is, the vertex having the greatest -coordinate among all the vertices). If the coordinates of that vertex are ), enter the value of .
The answer is 21.648.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose the intersection points with the x y plane are I 1 , I 2 , I 3 , and that the submerged vertex is P . The three vectors from P to I 1 , I 2 , I 3 must all be perpendicular.
( I 1 x − P x ) ( I 2 x − P x ) + ( I 1 y − P y ) ( I 2 y − P y ) + ( I 1 z − P z ) ( I 2 z − P z ) = 0 ( I 2 x − P x ) ( I 3 x − P x ) + ( I 2 y − P y ) ( I 3 y − P y ) + ( I 2 z − P z ) ( I 3 z − P z ) = 0 ( I 3 x − P x ) ( I 1 x − P x ) + ( I 3 y − P y ) ( I 1 y − P y ) + ( I 3 z − P z ) ( I 1 z − P z ) = 0
Solving this non-linear system and choosing the negative-z result gives ( P x , P y , P z ) ≈ ( − 3 . 6 3 6 1 , 5 . 5 1 8 6 , − 6 . 7 8 6 5 ) . It is then a fairly trivial matter to reconstruct the eight cube vertices using the side lengths and basis vectors consisting of unitized versions of ( I 1 − P ) , ( I 2 − P ) , ( I 3 − P ) . The highest vertex ends up being ≈ ( 1 . 3 2 3 5 , − 5 . 3 9 0 6 , 2 5 . 7 1 5 6 ) , and the sum of its coordinates is approximately 2 1 . 6 4 8 5 .