Going Around In A Discrete Harmonic Spiral
 A man is standing at the origin. First, he walks
1
unit in the positive
x
direction and reaches
(
1
,
0
)
. Then, he turns
6
0
o
counterclockwise and walks
1
/
2
units. Again, he turns
6
0
o
counterclockwise and walks
1
/
3
units. He continues this endlessly.
A man is standing at the origin. First, he walks
1
unit in the positive
x
direction and reaches
(
1
,
0
)
. Then, he turns
6
0
o
counterclockwise and walks
1
/
2
units. Again, he turns
6
0
o
counterclockwise and walks
1
/
3
units. He continues this endlessly.
Find the distance between his initial and final position.
The answer is 1.047.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Or we could have done it by the use of complex numbers. the sum would be: d = ∣ ∣ ∣ ∑ r = 0 ∞ r + 1 e i π r / 3 ∣ ∣ ∣ = ∣ ∣ ∣ 2 3 π + i 6 π ∣ ∣ ∣ ≈ 1 . 0 4 7 But even after solving it I entered , eventually the wrong answer due to calculation errors!!
Log in to reply
It's essentially the same thing.
Log in to reply
The problem with the man is that he had to walk infinite distance.
I used the same logic. I am attaching a graphic to show how the spiral looks like.
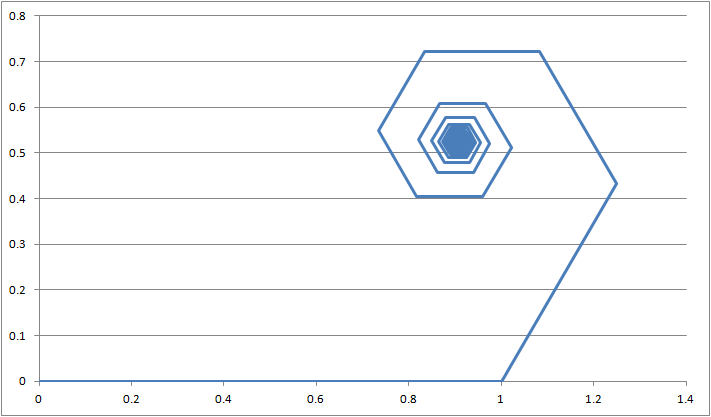
Nice! How did you generate the graphic?
Log in to reply
I just used a Microsoft Excel spreadsheet. It is easy.
∑ k = 1 ∞ k e ( k − 1 ) π i / 3 = − e − π i / 3 ln ( 1 − e π i / 3 ) = − e − π i / 3 ln ( 1 / 2 − i ( 3 ) / 2 ) = − e − π i / 3 ln e − π i / 3 = − e − π i / 3 ( − π i / 3 )
Which has modulus 3 π .
Let the unit vector along the + x direction be i ^ and that along the + y direction be j ^ . Let O be the origin.
The position vector of the final position (say P ) wrt O of the man is given by the vector sum of all the displacements, IE
O P = i ^ + 2 1 ( cos 3 π i ^ + sin 3 π j ^ ) + 3 1 ( cos 3 2 π i ^ + sin 3 2 π j ^ ) + ⋯ = ( 1 + 2 1 cos 3 π + 3 1 cos 3 2 π + ⋯ ) i ^ + ( 2 1 sin 3 π + 3 1 sin 3 2 π + ⋯ ) j ^ = S 1 ( n = 1 ∑ ∞ n 1 cos 3 ( n − 1 ) π ) i ^ + S 2 ( n = 1 ∑ ∞ n 1 sin 3 ( n − 1 ) π ) j ^ = S 1 i ^ + S 2 j ^
Clearly, S 1 = ℜ n = 1 ∑ ∞ n e i ( n − 1 ) π / 3 and S 2 = ℑ n = 1 ∑ ∞ n e i ( n − 1 ) π / 3
Let us evaluate S = n = 1 ∑ ∞ n e i ( n − 1 ) π / 3 .
For that, consider the Maclaurin expansion of ( 1 − x ) − 1 . ( 1 − x ) − 1 = n = 0 ∑ ∞ x n Integrate on LHS and RHS, note that the constant of integration is 0 , and then divide by x to obtain n = 0 ∑ ∞ n + 1 x n = n = 1 ∑ ∞ n x n − 1 = − x lo g ( 1 − x ) ( 1 ) Therefore from ( 1 ) , S = − e i π / 3 lo g ( 1 − e i π / 3 ) = 2 3 π + i 6 π
Hence, O P = ℜ { S } i ^ + ℑ { S } j ^ = 2 3 π i ^ + 6 π j ^
So, finally, ∣ O P ∣ = 3 π ≈ 1 . 0 4 7