Coordinated Artillery Barrage

Standard analysis of projectile motion: $t_\theta = \frac{2v_0}g\sin \theta; \\ R_\theta = \frac{2v_0^2}g\sin \theta\cos\theta = \frac{v_0^2}g\sin 2\theta.$ Two different angles result in the same range $R$ if $\sin\theta_1 = \cos\theta_2$ and vice versa. Let $\theta$ be the smaller angle (less than 45 degrees), then we have $t_{90^\circ-\theta} - t_\theta = \Delta t$ (the time difference between two launches $\Delta t \geq 60$ ). Substituting the given formulas and using $\sin(90^\circ-\theta) = \cos\theta$ , we find $\frac{2v_0}g(\cos\theta - \sin\theta) = \Delta t.$ Compare this with the range formula, and you realize that squaring this equation may be the thing to do: $\frac{4v_0^2}{g^2}(\overbrace{\cos^2 \theta + \sin^2 \theta}^{1} - 2\cos\theta\sin\theta) = (\Delta t)^2; \\ \frac{4v_0^2}{g^2} - \frac {4R}g = (\Delta t)^2; \\ R = \frac{v_0^2}g - \frac{g(\Delta t)^2}4.$ Obviously this is maximal for minimal $\Delta t = 60$ . Substitute the known values: $R = \frac{1000^2}{10} - \frac{10\cdot 60^2}4 = 100\:000 - 9\:000 = 91\:000\ \text{m}.$

Let $x, y$ be the horizontal and vertical components of the initial velocity. Then $x^2+y^2=1000^2$ as given. The time to reach the highest point equals $y/g$ ; hence, total flight time is $2y/g$ . Thus, the horizontal distance traveled is $2xy/g$ . So, to arrive at the same location, we can only swap $x,y$ . To maximize the distance, we need to minimize the difference between $x,y$ . Therfore, take $2y/g = 2x/g+60$ , as given; i.e. $y=x+30$ . Substitution in equation for initial velocity yields $x^2+(x+30)^2=1000^2$ This simplifies to $2x(x+30) = 1000^2-300^2$ Thus $2xy/g = (1000^2-300^2)/g=91000$ gives the solution.

Relevant wiki: Projectile Motion

Let $\theta_{1}$ and $\theta_{2}$ be the launch angles of the first and second shells, respectively. Now since the range of a projectile with initial speed $v$ and launch angle $\theta$ is $R = \dfrac{v^{2}}{g}\sin(2\theta)$ , for the two shells to land on the same target, (assuming that each is launched with the same initial speed), we must have that $\sin(2\theta_{1}) = \sin(2\theta_{2})$ . Now given that the shells are fired at least $60$ seconds apart we know that their launch angles will be unequal, so since $\theta_{1}, \theta_{2} \lt 90^{\circ}$ we must have that $2\theta_{1} = 180^{\circ} - 2\theta_{2} \Longrightarrow \theta_{1} + \theta_{2} = 90^{\circ}$ .

Now the vertical component of the motion of a projectile is given by $y = v\sin(\theta)t - \dfrac{1}{2}gt^{2}$ . Setting this to $0$ and solving for $t$ gives us the time from launch to impact as $t = \dfrac{2v}{g}\sin(\theta)$ . Letting $t = 0$ at the time of the launch of the first shell, with $v = 1000$ m/s and $g = 10$ m/s $^{2}$ we have that the time at the moment of impact of the first shell is $t = 200\sin(\theta_{1})$ . The second shell, being launched $T \ge 60$ seconds after the first, will be in the air for $200\sin(\theta_{2})$ seconds, so for the two shells to impact simultaneously we must have that

$200\sin(\theta_{1}) = 200\sin(\theta_{2}) + T \Longrightarrow \sin(\theta_{1}) - \sin(\theta_{2}) = \dfrac{T}{200} \Longrightarrow \sin(\theta_{1}) - \cos(\theta_{1}) = \dfrac{T}{200}$ ,

where $\sin(\theta_{2}) = \sin(90^{\circ} - \theta_{1}) = \cos(\theta_{1})$ . Squaring both sides leads to

$\sin^{2}(\theta_{1}) + \cos^{2}(\theta_{1}) - 2\sin(\theta_{1})\cos(\theta_{1}) = \dfrac{T^{2}}{40000} \Longrightarrow 1 - \dfrac{T^{2}}{40000} = \sin(2\theta_{1})$ .

Now the horizontal component of the motion of the projectile is given by $x = v\cos(\theta)t$ , so at the time of impact of the first shell

$x = v\cos(\theta_{1}) \times 200\sin(\theta_{1}) = 100000\sin(2\theta_{1}) = 100000\left(1 - \dfrac{T^{2}}{40000}\right)$ .

This is clearly maximized when $T$ is minimized, so

$x_{max} = 100000\left(1 - \dfrac{60^{2}}{40000}\right) = 100000\left(1 - \dfrac{9}{100}\right) = \boxed{91000}$ meters.

Suppose the two projectiles are fired at angles $\theta$ and $\phi$ , respectively. The first one fires with initial velocity $v_y = 1000\sin\theta$ and $v_x = 1000\cos\theta$ , and the second the same with $\phi$ instead of $\theta$ . The first one impacts the ground at time $\frac{1000\sin\theta}{5} = 200\sin\theta$ , and the second one at time $\frac{1000\sin\phi}{5}+60=200\sin\phi+60$ . This gives us one equation. $200\sin\theta+60=200\sin\phi$ We also know the impact distance must be the same, so we have $d = (1000\cos\theta)( 200\sin\theta) = (1000\sin\phi)(200\cos\phi) \implies \sin2\theta=\sin2\phi$ This happens when $2\theta = \pi-2\phi \implies \theta = \frac{\pi}{2}-\phi$ . This means $\sin\theta=\cos\phi$ .

Plugging this back in to $200\sin\theta+60=200\sin\phi$ gives us that $200\cos\phi+60=200\sin\phi$ $\cos\phi+.3=\sin\phi$ $\cos\phi-\sin\phi=-.3$ $\cos^2\phi-2\sin\phi\cos\phi+\sin^2\phi=.09$ $2\sin\phi\cos\phi = 0.91$

We know $d =(1000\sin\phi)(200\cos\phi)= 100000(2\sin\phi\cos\phi) = 91000$

Thus the distance is $\boxed{91000}$

From:

$\begin{cases} x = v\ cos(\theta)\ t \\ v_x = v\ cos(\theta) \end{cases}$

$\begin{cases} y = - \frac{1}2\ g\ t^2\ +\ v\ sin(\theta)\ t \\ v_y = v\ sin(\theta)\ -\ g\ t \\ a = -g \end{cases}$

it follows:

$range(\theta) = \frac{v^2}g\sin(2\theta) \\ \Delta t(\theta) = \frac{2v}g\sin(\theta)$

having those drawings:

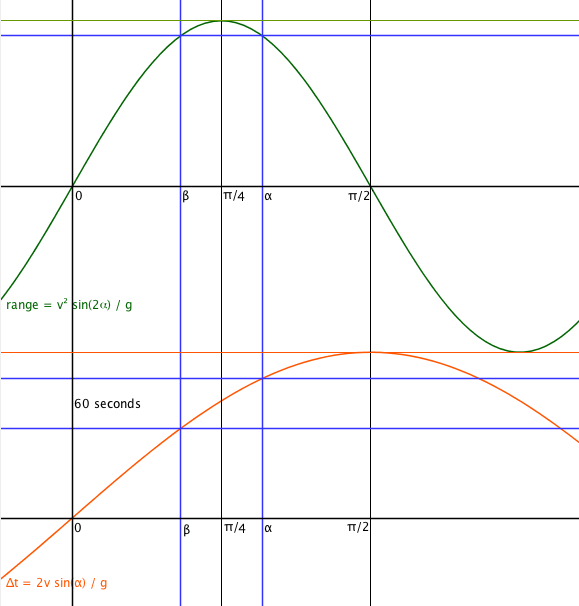
The two angles I am looking for are $\alpha$ and $\beta$ that have to fullfill the following two restrictions:

• they must provide the same range (the blue horizontal line crossing the green drawing)

• they must fullfill $\Delta t(\alpha)\ =\ \Delta t(\beta)\ +\ 60$ as described in blue around the red drawing.

Those conditions are described by:

$\begin{cases} \frac{v^2}g\ sin(2\alpha) = \frac{v^2}g\ sin(2\beta) \\ \frac{2\ v}g\ sin(\alpha) = \frac{2\ v}g\ sin(\beta)\ +\ 60 \end{cases}$

From the first equation and looking at the drawing it comes out that:

$\frac{\pi}4\ - \beta\ =\ \alpha\ - \frac{\pi}4$

so

$\beta\ =\ \frac{\pi}2\ -\ \alpha$

and this changes the second equation in:

$sin(\alpha)\ =\ cos(\alpha)\ +\ \frac{60\ g}{2\ v}$

Now set:

$\begin{cases} Y\ = sin(\alpha) \\ X\ = cos(\alpha) \end{cases}$

and resolve:

$\begin{cases} Y\ =\ X\ +\ \frac{60\ g}{2\ v} \\ X^2\ +\ Y^2 = 1 \end{cases}$

The solution, using parameters provided in the quiz, is:

$\begin{cases} X = \frac{\sqrt{191}\ -\ 3}{20} \\ Y = \frac{\sqrt{191}\ + \ 3}{20} \end{cases}$

Now, by replacing those values into the definition of range:

$range(\alpha) = \frac{v^2}g\sin(2\alpha) = \frac{2\ v^2}g\sin(\alpha)\cos(\alpha) = \frac{2\ 000\ 000}{10}\frac{\sqrt{191}\ + \ 3}{20}\frac{\sqrt{191}\ -\ 3}{20} = 91\ 000\ m$

T=2usin∆/g.................................................. .......{∆=angle with horizontal &. u=1000}

T-60 =2sin(π\2-∆)/g ~~~~~~~~EXPLANATION:

As the digram suggests the ranges must be same, it will be same if initial angle is same but as it is mentioned it is different so,

R=R'(R=range)

u^2sin2∆/g. =. u^2sin∆'/g<<<<<<<<clearly if ∆=∆' or >>>∆'=π\2-∆<<<

And also the second cannon is launched after 60 seconds (keeping in SI system)

So for second cannon time must be 60 seconds less than the first cannon and also the angle must be different (π\2-∆)

Solving we get any of them(sin∆ & cos∆)

Put that in .....>>>>>>>>>R=2ucos∆usin∆\g

(THERE ARE BETTER SOLUTIONS THAN THIS; TO AVOID MORE CALCULATION)