Coordinated Polygons II
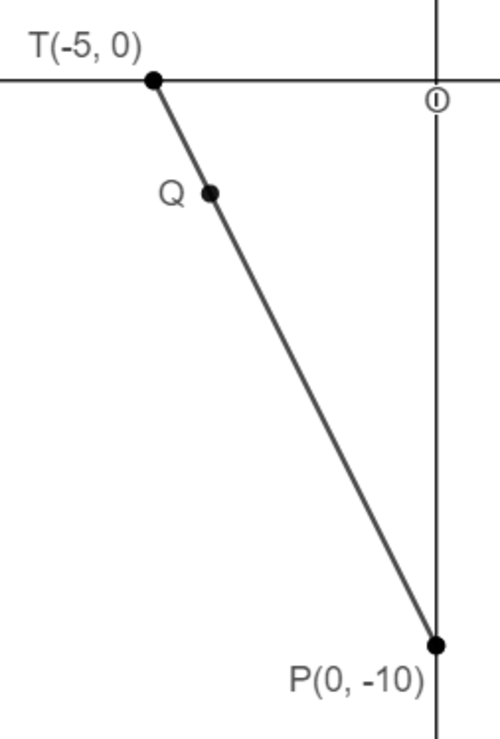
In the figure shown, point Q lies on the straight line T P such that T Q : Q P = 1 : 4 . Calculate the area of △ O Q P .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
The ratio of 1:4 tells us that the coordinates of Q are (-2,-4) so it becomes a simple calculation for area = 1/2 × Base x Height.
Log in to reply
Pretty sure the coordinates of Q are (-4,-2).
I think this is the only solution which has not "assumed" that OQ is perpendicular to TP but still proves that area of OQP is four fifth of TOP thus making it 20.
If I understand the solution correctly then for any right angle triangle ABC with AC being hypotenuse for any point D on AC connected to B following will always hold true.
area of ABD:area of CBD :: AD:CD
Correct me please if I am wrong.
Log in to reply
Yes, this is correct. Both ABD and CBD would have the same height, so the area is only affected by the bases AD and CD, so the ratios are the same.
Pardon my ignorance and correct me if I am wrong because my formal education in maths and geometry is only equivalent to O levels but in some fields I can give correct answers to 70 to 80 of problems in Brilliant and on the average it is about 40 to 50 percent. Having said that now on further thinking I think my statement is correct for any triangle whether it is right angled or not and I think I do have a proof for it as well.
This was simple...
how did he prove they are similar? angle RQO is congruent to angle QOT but what about the other angles?
Log in to reply
∠ P is congruent to itself, and ∠ T is congruent to ∠ R Q P by corresponding angles.
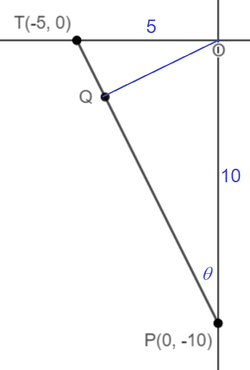
From the coordinates we note that O P = 1 0 and O T = 5 . By Pythagorean theorem we have T P 2 = O T 2 + O P 2 = 5 2 + 1 0 2 ⟹ T P = 5 5 . Since T Q : Q P = 1 : 4 , Q P = 5 4 T P = 5 4 × 5 5 = 4 5 . Then, the area of △ O Q P is given by:
A = 2 1 × Q P × O P × sin ∠ T P O = 2 1 × 4 5 × 1 0 × 5 5 5 = 2 0
The diagram looks like this:
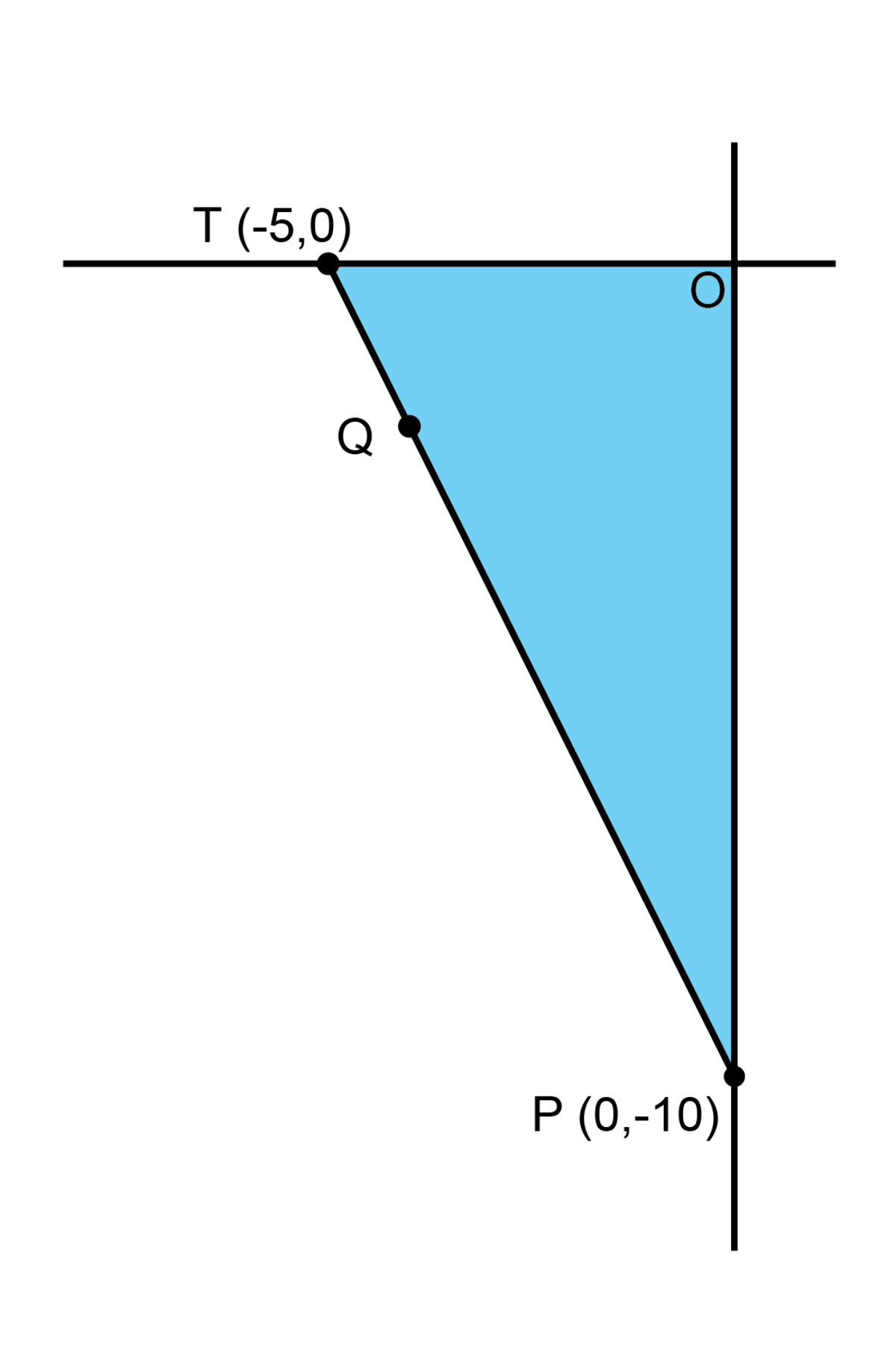
If we rotate the blue triangle and drop a perpendicular from point O we get:
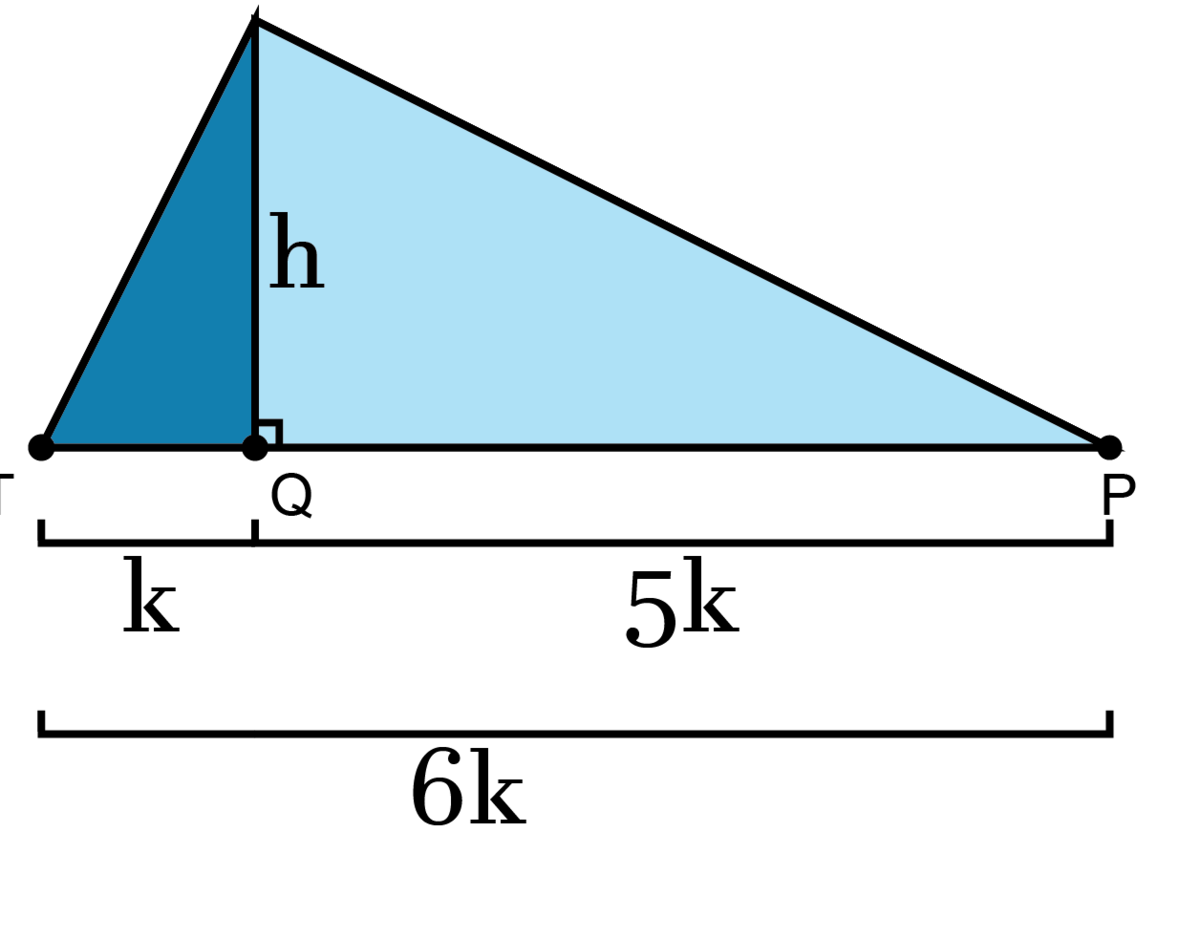
The light blue triangle △ O Q P and the big triangle △ O T P both have the same height h , but the light blue triangle has 5 4 the base of the large triangle.
Therefore, △ O Q P has 5 4 the area of △ O T P . The area of △ O T P = 2 5 × 1 0 = 2 5
Thus the area of △ O Q P = 2 5 × 5 4 = 2 0
This solution is based on the assumption that OQ is perpendicular to TP which might be true in this case but cannot be presumed by the given information and if needed should be proven first.
This problem can be solved without finding out the value of any additional lengths.
Given the coordinates of T and P, the area of △OTP = 2 1 ⋅ 5 ⋅10 = 25
Construct height OH, with TP as the base of the triangle, OH is the height for both △OQT and △OQP Since TQ:QP=1:4, the ratio between area of △OQT and area of △OQP is also 1:4 (they have the same height, OH)
Therefore, area of △OQP = 1 + 5 4 ⋅ 25 = 20
(The area of two triangles are the same if the corresponding base and height of the two triangles have the same length. If a ratio exists, the areas have the same ratio as their bases or heights)
Consider TP the base of the TOP triangle, which has an area of 25. OQP triangle is 80% of TOP (that is, 4/5, as is has 4/5 of the base of TOP). Therefore the area of OQP is 20.
Using the same assumption as above.
Draw a line OH perpendicular to the TP. Thus,we can know that S {△OTP}=0.5*TP*OH=25 and S {△OQP}=0.5 OH QP. Since we have TQ:QP=1:4,we can get S {△OTP}: S {△OQP}=TP:QP=5:4 So S_{△OQP}=20
Draw Q R parallel to O T so that R is on O P .
Then △ P Q R ∼ △ P T O by AA similarity, so Q P T P = Q R T O , or 4 1 + 4 = Q R 5 , or Q R = 4 .
Therefore, the area of △ O Q P is A = 2 1 ⋅ O P ⋅ Q R = 2 1 ⋅ 4 ⋅ 1 0 = 2 0 .