Coordinates of point $F$

The inradius is $r=\frac{3+4-5}{2}=1$ . Putting an origin at $A$ , the point $F$ lies on the angle bisector of $\angle BCD$ and on the line $y=1$ .

So $F$ has coordinates $F \left(3+\cot \frac{\angle BCD}{2},1 \right)$

We have $\angle BCD = \pi-\angle ACB$ and $\tan \angle ACB=\frac43$ . Hence $\cot \frac{\angle BCD}{2}=\frac12$ and $F\left(\frac72,1\right)$ giving the answer $\boxed{4.5}$ .

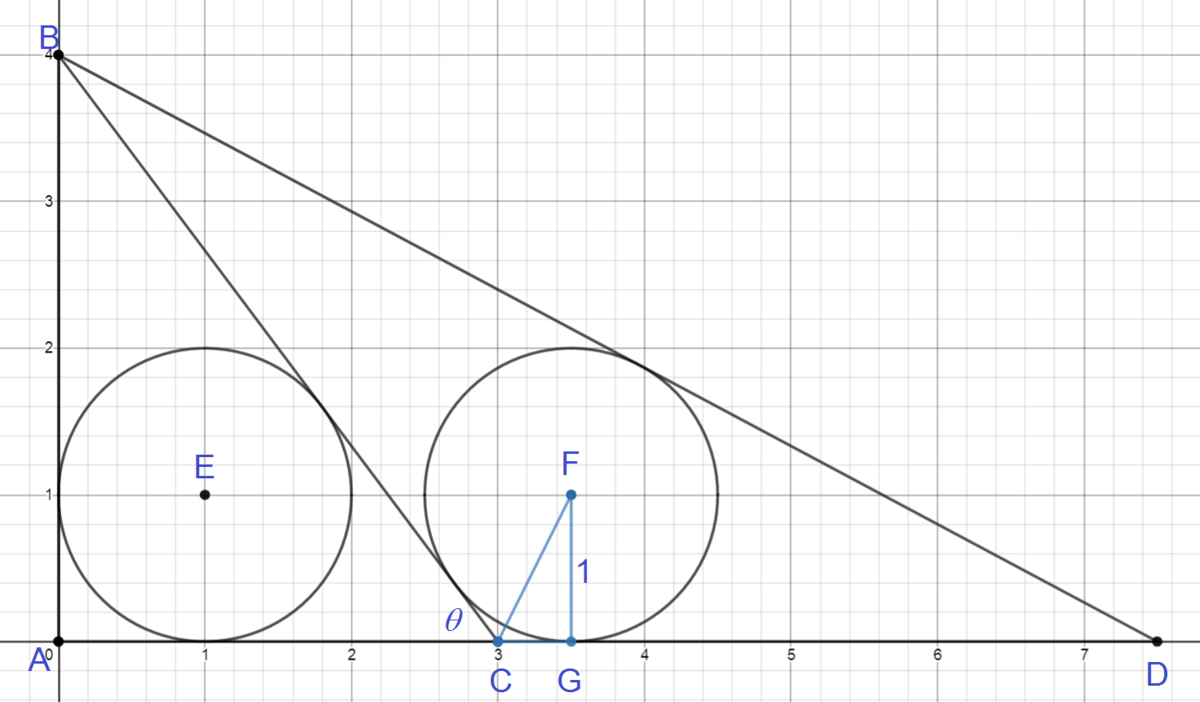
$\triangle ABC$ is a $3$ - $4$ - $5$ triangle, therefore $BC=5$ . Then the area of triangle $[ABC] = \dfrac {4 \times 3}2 = 6 = sr$ , where $s$ is the semiperimeter of the triangle and $r$ , the radius of the incircle. Therefore $\dfrac {3+4+5}2 r = 6 \implies r = 1$ , Let $FG$ be perpendicular to $AD$ . Then $y = FG = 1$ . And

$\begin{aligned} x & = AG = AC + CG = 3 + FG \cdot \cot \blue{\angle FCD} & \small \blue{\text{Note that }\angle FCD = \frac {\angle BCD}2} \\ & = 3+ \cot \blue{\left(\frac {\angle BCD}2 \right)} = 3+ \cot \left(\frac {180^\circ - \red{\angle BCA}}2 \right) & \small \red{\text{Let }\angle BCA = \theta} \\ & = 3 + \cot \left(90^\circ - \frac \red \theta 2 \right) = 3 + \tan \frac \theta 2 = 3 + \frac {1-\cos \theta}{\sin \theta} \\ & = 3 + \frac {1-\frac 35}{\frac 45} = 3 + \frac 12 = 3.5 \end{aligned}$

Therefore $x+y = 3.5 + 1 = \boxed{4.5}$ ,

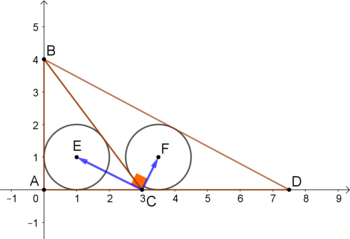The inradius of the $3$ - $4$ - $5$ right triangle is equal to 1, hence point $E$ has coordinates $\left( 1,1 \right)$ . Since the two circles are congruent, the y-coordinate of $F$ is equal to 1. Let $x$ be the x-coordinate of $F$ .

Focusing on the vectors $\overrightarrow{CF}=\left( \begin{matrix} {{x}_{F}}-{{x}_{C}} \\ {{y}_{F}}-{{y}_{C}} \\ \end{matrix} \right)=\left( \begin{matrix} x-3 \\ 1-0 \\ \end{matrix} \right)=\left( \begin{matrix} x-3 \\ 1 \\ \end{matrix} \right)$ and $\overrightarrow{CE}=\left( \begin{matrix} {{x}_{E}}-{{x}_{C}} \\ {{y}_{E}}-{{y}_{C}} \\ \end{matrix} \right)=\left( \begin{matrix} 1-3 \\ 1-0 \\ \end{matrix} \right)=\left( \begin{matrix} -2 \\ 1 \\ \end{matrix} \right)$ , we have

$\overrightarrow{CF}\bot \overrightarrow{CE}\Leftrightarrow \overrightarrow{CF}\cdot \overrightarrow{CE}=0\Leftrightarrow \left( \begin{matrix} x-3 \\ 1 \\ \end{matrix} \right)\left( \begin{matrix} -2 \\ 1 \\ \end{matrix} \right)=0\Leftrightarrow -2\left( x-3 \right)+1=0\Leftrightarrow x=3.5$ Hence, ${{x}_{F}}+{{y}_{F}}=3.5+1=\boxed{4.5}$ .

From the previous problem, we found that $\overline{CD} = 4.5$

Therefore, the coordinates of the vertices of $\triangle BCD$ are

$B(0, 4) , C(3, 0), D(7.5, 0)$

And the side lengths are $b = 4.5 , c = \sqrt{4^2 + 7.5^2} = 8.5 , d = 5$

Hence, the coordinates of the incenter $F$ are

$F = (x, y) = \dfrac{b}{b + c + d} B + \dfrac{c}{b + c + d } C + \dfrac{d}{b+c+d} D$

Substituting the numerical values,

$(x, y) = \dfrac{4.5}{18} (0, 4) + \dfrac{8.5}{18} (3, 0) + \dfrac{5}{18}(7.5, 0) = (0, 1) + ( \dfrac{17}{12} , 0 ) + (\dfrac{25}{12} , 0) = ( \dfrac{7}{2} , 1 ) = (3.5, 1)$

Hence $x + y = \boxed{4.5}$