Cops and robbers 2
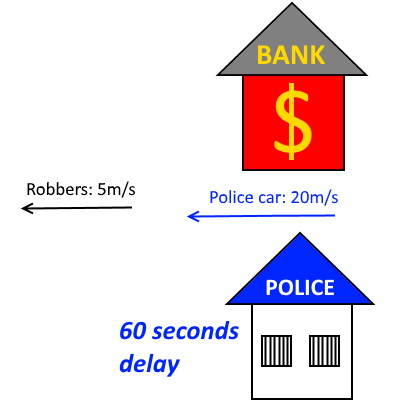
20 robbers have robbed a bank, and each of them starts running away with the speed of 5 m/s. 60 seconds after the robbers started running, a police car in the police station opposite to the bank start chasing the robbers with the speed of 20 m/s. As there is only space for one robber to carry in the police car, only one robber at a time can be arrested and taken to the police station.
How many seconds does it take the police to arrest all 20 robbers and take them to the police station? If the time it takes is in seconds, give the answer as where denotes the floor function .
Details and assumptions:
- The delay of 60 seconds doesn't count to the final result.
- Only the trips to catch robbers and take them to the police station take time. Arresting robbers and leaving them at the station don't take time.
- The police station is assumed to be located in the same place as the bank.
Click the link for the original version of this problem, Cops and robbers 1
The answer is 1641006.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let t 1 be the time it takes to catch the first robber and take him to the police station. The overall metres travelled by the first robber doubled (because this doesn't include the trip back which is equally long) equals the metres travelled by the police at their first sprint. The first robber travels 60 seconds plus half of t 1 (as the other half goes driving back to the police station) with 5 m/s, and the police car travels t 1 seconds with 20 m/s.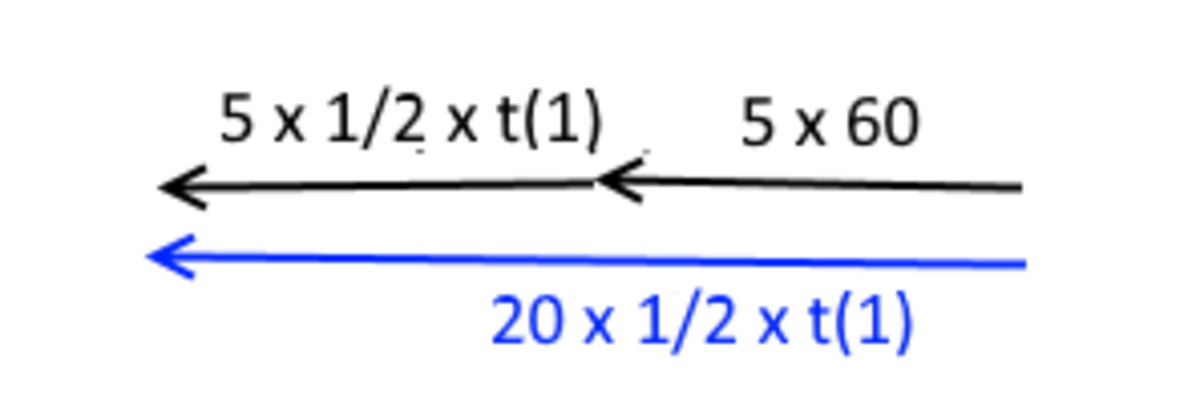
s = 2 × 5 × ( 6 0 + 2 1 t 1 ) = 2 0 t 1
6 0 0 + 5 t 1 = 2 0 t 1
1 5 t 1 = 6 0 0
t 1 = 4 0
The second robber travels 60 seconds plus t 1 (which was spent catching the first robber) plus half t 2 (as the other half goes to the trip back to station) with 5 m/s. After doubled (because it doesn't include the trip back which is equally long), it equals the amount of metres travelled by the police car at the second sprint, which is 20 m/s times t 2 .
2 × 5 × ( 6 0 + t 1 + 2 1 t 2 ) = 2 0 t 2
6 0 0 + 1 0 t 1 + 5 t 2 = 2 0 t 2
1 5 t 2 = 6 0 0 + 1 0 × 4 0
t 2 = 1 5 1 0 0 0 = 3 5 × t 1
From now on, for each ínteger n where n > 1 , we get the time spent to the n th sprint (to catch the n th robber and take him to the police station) = t n is
2 0 t n = 2 × 5 × ( 6 0 + k = 1 ∑ n − 1 ( t k ) + 2 1 t n )
2 0 t n = 6 0 0 + 1 0 k = 1 ∑ n − 1 ( t k ) + 5 t n
1 5 t n = 6 0 0 + 1 0 k = 1 ∑ n − 1 ( t k )
Which also means
2 0 t n + 1 = 2 × 5 × ( 6 0 + k = 1 ∑ n ( t k ) + 2 1 t n + 1 )
2 0 t n + 1 = 6 0 0 + 1 0 k = 1 ∑ n ( t k ) + 5 t n + 1
1 5 t n + 1 = 6 0 0 + 1 0 k = 1 ∑ n − 1 ( t k ) + 1 0 t n = 1 5 t n + 1 0 t n
t n + 1 = 3 5 × t n
By looking at t 1 , t 2 and the result above, we see that the times t n form a geometric progression where t n = t 1 × ( 3 5 ) n − 1 = 4 0 × ( 3 5 ) n − 1 . The total time spent is the sum of times spent for each robber:
t = i = 1 ∑ 2 0 ( t i ) = i = 1 ∑ 2 0 ( 4 0 × ( 3 5 ) i − 1 ) = 1 − 3 5 4 0 ( 1 − ( 3 5 ) 2 0 ) = 1 6 4 1 0 0 6 . 3 6 6 7 5 3
We get ⌊ t ⌋ = 1 6 4 1 0 0 6 .