Cops and robbers 1

Algebra Level pending

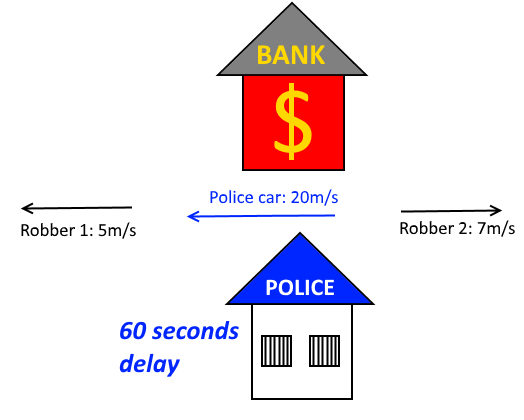
Two robbers have robbed a bank and start running to distinct directions. One runs to West with the speed of 5 m/s, and the other runs to East with the speed of 7 m/s. 60 seconds after the robbers started running away, the police in the police station opposite to the bank start chasing the robbers with the speed of 20 m/s. The police first arrests the robber going to West.

How many seconds does it take the police to arrest both robbers and take them to the police station? If the time is t t seconds, give the answer as ⌊ t ⌋ \lfloor t\rfloor where ⌊ ⌋ \lfloor \rfloor denotes the floor function .

Details and assumptions:

  • The delay of 60 seconds doesn't count to the final result.
  • Arresting the robbers and leaving them at the police station don't take time. Only the trips take time.
  • The bank and the police station can be assumed to be located in the same place.

Click the link for the harder version of this problem, Cops and robbers 2


The answer is 147.

Tarmo Taipale by Tarmo Taipale , 22, Finland

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Tarmo Taipale
Dec 4, 2016

Let t 1 t_1 be the time it takes the police car to catch the first robber. Taking the speed of the police car (20 m/s) and the robber (5m/s) and the 60 seconds delay to the count, the amount of metres both the robber and the police car travel is

s = 20 t 1 = 5 × 60 + 5 t 1 s=20t_1=5\times60+5t_1

We get

15 t 1 = 300 15t_1=300

t 1 = 20 t_1=20 .

Now we know that it takes the police car 20 seconds to catch the first robber and another 20 seconds to get back to the police station and drop the robber. All this time the second robber has run with 7 m/s and the police start catching them.

Now let t 2 t_2 be the time in seconds it takes the police to arrest the second robber in their second trip. The amount of metres travelled by the second robber and the police is

s = 20 t 2 = 7 × ( 60 + 2 t 1 + t 2 ) s=20t_2=7\times{(60+2t_1+t_2)}

We get

13 t 2 = 7 × 60 + 7 × 2 × 20 = 700 13t_2=7\times60+7\times2\times20=700

t 2 = 700 13 t_2=\frac{700}{13}

The total time is t = 2 t 1 + 2 t 2 = 2 × 20 + 2 × 700 13 = 147.692 t=2t_1+2t_2=2\times20+2\times\frac{700}{13}=147.692

⌊ t ⌋ = 147 \lfloor t\rfloor = \boxed{147} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...