Corrcect odd primes are wanted
How many odd primes are there such that is a divisor of
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Notation: [x] is the largest integer less than or equal to a real number x.
If p is a divisor of k,then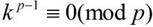
Otherwise ,by Fermat's little thorem
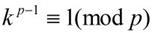So we see that
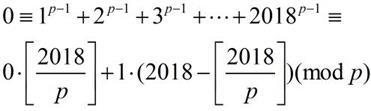since [2018/p] is exactly the number of multipliers of p between 1 and 2018. This means
......(※)
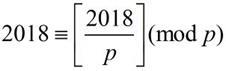We see that p<2019,because p≥2019 means [2018/p] will be zero,and so p becomes a divisor of 2018,contradictio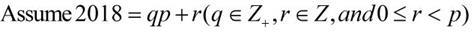n.
Then
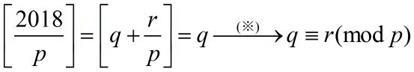Two cases to be discussed:
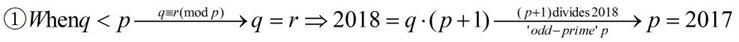
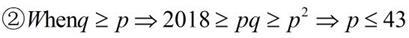_ in this case we only need to check one by one,
as p∈{3,5,7,11,13,17,19,23,29,31,37,41,43} and must satisfy (※).The result turns out that p=5 or 31 .
Therefore,the answer is 3.( only p=5, 31, 2017 )