Correct Propagation
Geometry
Level
1
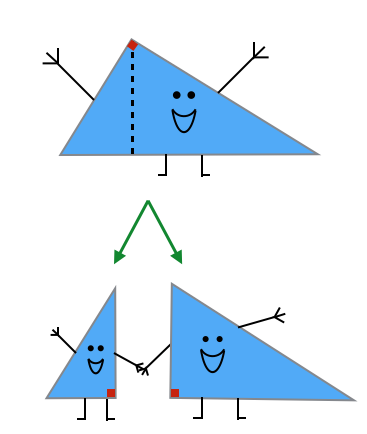If you use a single, straight cut to make any one right triangle into two, smaller right triangles; what can you say about the two offspring triangles in comparison to their parent?
Neither offspring can be similar to the parent.
Both offspring are definitely similar to the parent.
You cannot conclude any of the other options for certain.
The larger of the two offspring will be similar to the parent and the smaller will not be similar.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Let's say you have a right triangle with other angles x and y. If you cut it into two right triangles, you had to have split the right angle with a line that is also perpendicular to the hypotenuse. This leaves you, in each triangle, an unknown angle from cutting the right angle in two, a new right angle, and either x or y for the third angle. Since a triangle has a total of 180 degrees in its angles, that means the the unknown angle must either be x if in the triangle with known angle y, or y if the known angle is x. Thus, both triangles are similar to the original.