Correlations and temperature
Phase transitions, like from liquid to solid, are familiar in everyday experience. More exotic phase transitions, such as the change of a conductor to a superconductor, are characterized by a "correlation length." The correlation length is the length over which properties of the system look the same.
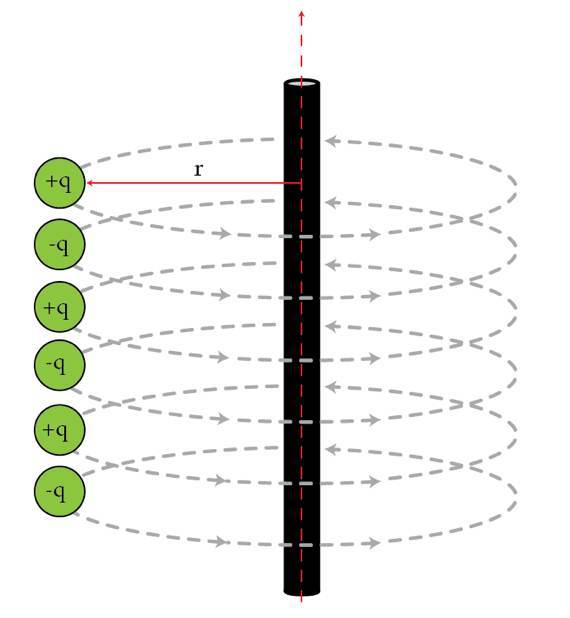
As a simple example, consider a line of alternating charges ( + q and − q ), connected by small nonconducting rods to a long vertical rod, as in the figure below. In cylindrical coordinates the charges are at r = R , z = … − 2 , − 1 , 0 , 1 , 2 … and can only rotate around the long rod, i.e. they can only move in θ . At absolute zero, none of the charges can ever have any kinetic energy. Therefore they must all be in their lowest energy state, with all the small rods aligned. Hence for absolute zero the correlation length is infinity, in that if I measure the angle θ of one rod, I know the angle θ for a rod an infinite distance away.
If we increase the temperature, then the rods will start to wiggle back and forth. At very high temperatures, the rods are spinning around like mad, and so measuring the angle θ for one rod tells us nothing about the rod right next to it. In this case the correlation length is zero. The phase transition in this situation is from an uncorrelated or disordered system at non-zero temperature, to a completely ordered system at absolute zero.
Correlation lengths generically diverge with temperature as L ∝ ∣ T − T c ∣ − ν , where T c is a critical temperature (in our case absolute zero for simplicity), T is near T c and ν is a positive number. If we define L for our case as the minimum number of rods between two rods that are oppositely aligned, what is ν for very low temperatures?
This problem is in memoriam of Kenneth Wilson , who developed much of what we know about phase transitions and passed away two weeks ago.
Details and assumptions
- For simplicity, only consider nearest neighbor interactions between the charges.
- Ignore gravity.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
A given state of the infinite stack of rotating charges is just one configuration out of the infinite set of possible configurations of the angles { … , θ − 1 , θ 0 , θ 1 , … } .
Of the many possibilities, the stack will tend to occupy the configurations that have the most favorable free energies, i.e. P ( θ ) ∼ e − F ( θ ) / k B T . As T → 0 , lower and lower energy states are occupied until only the lowest possible energy state can be occupied.
The free energy F of two interacting charges i and i + 1 is given by r i , i + 1 k q i q i + 1 .
For the stack, every charge contributes − 2 k r i , i + 1 q 2 (one interaction for each of its two neighbors).
The distance between two adjacent charges is approximately 1 + R 2 θ 2 and so the free energy per charge site is given by
F s i t e = − 2 k 1 + ( R θ ) 2 q 2 ≈ − 2 k q 2 ( 1 − R 2 θ 2 )
The probability of a particular configuration is then given by
P ( θ ) ∼ exp − k B T F s i t e = exp 2 k q 2 k B T 1 − R 2 θ 2 (for small θ ) ∼ exp − 2 k q 2 k B T R 2 θ 2
Therefore, the probability of the angle between adjacent charges has the general form P ( θ ) ∼ e − A θ 2 / T .
At T = 0 the probability becomes zero for all angles except for θ = 0 , as stated in the problem description. At temperatures slightly above zero, other configurations open up to the system but the system is still cut off from θ 2 much greater than T because the probability falls off dramatically for θ much beyond k B T . In other words, the partition function is dominated by the region where θ ∼ T . Therefore, the size of θ s i t e scales as T .
The correlation length L is defined as the number of rods in a half turn of the helical stack (a shift of π ), i.e.
L ≈ π / θ s i t e ∼ 1 / T = T − T c 1 .
Therefore, the exponent ν is 2 1 .
At T the avarage angle between the two adjacent rods is θ, then the potential energy E=-kq^2/sqrt(1+(θR)^2). At T=0, E(0)=-kq^2.
For θ <<1, E= -kq^2 + [k(qR)^2/2] θ^2, Compared with the mininum energy at absolute 0, T= E-E(0) = C θ^2, where C is a constant = [k(qR)^2/2].
Hence θ ∝ T^(1/2). L ∝ 1/θ ∝ T^(-1/2). Namely, ν = 1/2
Suppose the diffence in angle \theta between two consecutive rods is \alpha (alpha is small because T is small), the speed of each charge is v. According to kinetic theory of gases: \frac{m * v^2}{2} = \frac{3 * k_B * T}{2}
Hence m * v^2 = 3 * k_B * T
Because \alpha is small, we suppose the distance between two consecutive charges is d, which is the distance between the planes containing the orbit of each charge. Therefore, the attractive force between two consecutive charges is F_0 = \frac{k * q^2}{d^2}
The projection of this force into the plane containing the orbit of the charge: F
p = F
0 * \sin \gamma where \gamma is the angle between the vertical axis and the straight line connecting two consecutive charges.
Since \alpha is small, \sin \gamma = \frac{r * \alpha}{d}.
Therefore, F_p = \frac{k * q^2 * r * \alpha}{d^3}
The total force on each charge is: F = 2 * F_p * \sin \frac{\alpha}{2}
Since \alpha is small, F \approx F_p * \alpha = \frac{k * q^2 * r * \alpha^2}{d^3}
According to Newton Law II, F = \frac{m * v^2}{r} = \frac{3 * k_B * T}{r}
Therefore \alpha^2 = \frac{3 * k_B * T * d^3}{k * q^2 * r^2}
Therefore L = \frac{2 * \pi}{\alpha} = 2 * \pi * q * r * sprt{\frac{k}{3 * k_B * T * d^3}}
Therefore L \sim T^(-0.5) or v = 0.5
The equipartition theorem states that the average kinetic energy is E ∝ k T , where k is Boltzmann's constant. We can therefore say that the total energy per charge ABOVE the ground state energy is also ∝ k T . Since T is very small the charges will in general be almost aligned. The potential energy between a pair of charges that is exactly aligned is given by
E = − 1 K q 2
while the potential energy for a pair that is almost aligned is
E = − ( 1 + ( R Δ θ ) 2 ) 1 / 2 K q 2
where Δ θ is the misalignment angle between the charges. Δ θ is small, and so for a misaligned pair the potential energy above the ground state is
Δ E = 2 K q 2 R 2 ( Δ θ ) 2 ∝ k T .
If the Nth particle is oppositely aligned from the 0th particle, then Δ θ = π / N . Substituting this into the expression above yields N ∝ T − 1 / 2 which gives ν = 1 / 2 .
I had a question. Even at a low temperature, the charges should have a kinetic energy due to oscillations. But, why are we ignoring it here?
It is obvious that for cold temperatures that the angles are to be small and therefore that the energetics is given by a quadratic in the shape of − θ 2 multiplied by some constant. For these reasons, and the symmetry of the problem, we can now see that the distribution for the angles is given by the Boltzmann formula making for P ( θ ) = e − θ 2 / T . Of course there are multiplying factors but of no importance to the fact we are trying to solve.
Taking the average the full range from − ∞ to + ∞ and knowing that the errors due to this range extension are very small, the average angle can be solved for
⟨ θ ⟩ = − ∞ ∫ + ∞ e − θ 2 / T d θ − ∞ ∫ + ∞ θ 2 e − θ 2 / T d θ = 2 T .
Then so, the angle of each move is proportional to T , the total links to move an angle so that we are in anti-alignment with the starting rod must be proportional to the inverse 1 / T . The answer is now easy to see.