$\cos 36^\circ$

Let $\theta=18^\circ$ so that $2\theta=36^\circ$ and $3\theta=54^\circ$ so, $\cos54^\circ=\cos(90^\circ-36^\circ)=\sin36^\circ$ Or we can write it as $\cos3\theta=\sin2\theta$ Let’s see $\sin2\theta=2\sin\theta\cos\theta\\=2\cos\theta\sqrt{1-\cos^2\theta}$ Denote $\cos\theta=x$ We have $\sin2\theta=2x\sqrt{1-x^2}$ And we have $\cos3\theta=4cos^3\theta-3\cos\theta=4x^3-3x$ Then, $2x\sqrt{1-x^2}=4x^3-3x\\16x^4-20x^2+5=0$ We denote $y=x^2$ $16y^2-20y+5=0$ So we get $x^2=y_{1,2}=\frac{5\pm\sqrt5}{8}$ We discard the smaller root. And by double angle formula $\cos2\theta=2\cos^2\theta-1\\=2x^2-1\\=\frac{1+\sqrt5}{4}$

Consider a pentagram with an exterior regular pentagon $ABCDE$ with unit sides and an interior regular pentagon $FGHIJ$ with $x$ sides:

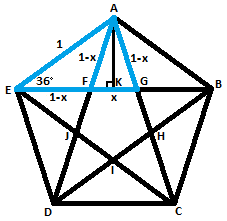
By symmetry, $AE = EG = 1$ , so $EF = EG - FG = 1 - x$ . Also by symmetry, $EF = AF = AG = 1 - x$ .

As interior angles of a regular pentagon, $\angle JFG = \angle EAB = 108°$ , so by vertical angles $\angle EFA = 108°$ , and as base angles of an isosceles $\triangle EFA$ , $\angle AEF = \angle EAF = \frac{1}{2}(180° - 108°) = 36°$ . Also by symmetry, $\angle GAB = \angle EAF = 36°$ , so $\angle GAF = \angle EAB - \angle EAF - \angle GAB$ $=$ $108° - 36° - 36° = 36°$ . Therefore, $\triangle EAG \sim \triangle AFG$ by SAS similarity.

Since $\triangle EAG \sim \triangle AFG$ , $\frac{AE}{AG} = \frac{AG}{FG}$ or $\frac{1}{1 - x} = \frac{1 - x}{x}$ , which solves to $x = \frac{3 - \sqrt{5}}{2}$ for $x < 1$ .

From right $\triangle AEK$ , $\cos \angle AEK = \frac{EK}{AE}$ , or $\cos 36° = \frac{1 - x + \frac{1}{2}x}{1}$ . Substituting $x = \frac{3 - \sqrt{5}}{2}$ from above and simplifying gives $\cos 36° = \boxed{\frac{1 + \sqrt{5}}{4}}$ .

Using the identity: $\displaystyle \sum_{k=1}^n \cos \left(\frac {2k-1}{2n+1}\pi \right) = \frac 12$ ,

$\begin{aligned} \cos \frac \pi 5 \color{#3D99F6} + \cos \frac {3\pi}5 & = \frac 12 & \small \color{#3D99F6} \text{Note that }\cos (\pi - \theta) = - \cos \theta \\ \cos \frac \pi 5 \color{#3D99F6} - \cos \frac {2\pi}5 & = \frac 12 & \small \color{#3D99F6} \text{and }\cos 2 \theta = 2 \cos^2 \theta - 1 \\ \cos \frac \pi 5 - 2 \cos^2 \frac \pi 5 + 1 & = \frac 12 \\ 4 \cos^2 \frac \pi 5 - 2 \cos \frac \pi 5 - 1 & = 0 \\ \implies \cos \frac \pi 5 & = \boxed{\dfrac {1+\sqrt 5}4} & \small \color{#3D99F6} \text{Since }\cos \frac \pi 5 > 0 \end{aligned}$

In a $3-4-5$ right triangle, the smallest angle is $37^\circ$

So, $cos37^\circ=\frac{4}{5}=0.8$

As $cosx$ decreases with increase in $x$ $(0^\circ \leq x\leq 90^\circ )$ and $36^\circ <37^\circ$ , the only option greater than $0.8$ is $\boxed{\frac{1+\sqrt{5}}{4}}$

$\cos 36\degree \approx 0.8$ , so we have to just find its approximation.

Then, it is $\displaystyle \boxed { \frac { 1 + \sqrt { 5 } } { 4 } }$ .