Cos the limit is funny

Calculus Level 3

$\begin{aligned} f(x) &=& \dfrac{1-\cos(1-\cos x)}{x^4} , x \neq 0 \\ f(0) &=& a \end{aligned}$

The function $f(x)$ is defined as above. If $f(x)$ is continuous everywhere, then $a$ is equal to $\dfrac{A}{B}$ for coprime positive integers $A$ and $B$ , find $A+B$ .

Try my set .

5 17 9 3

2 solutions

Raj Rajput
Jun 30, 2015

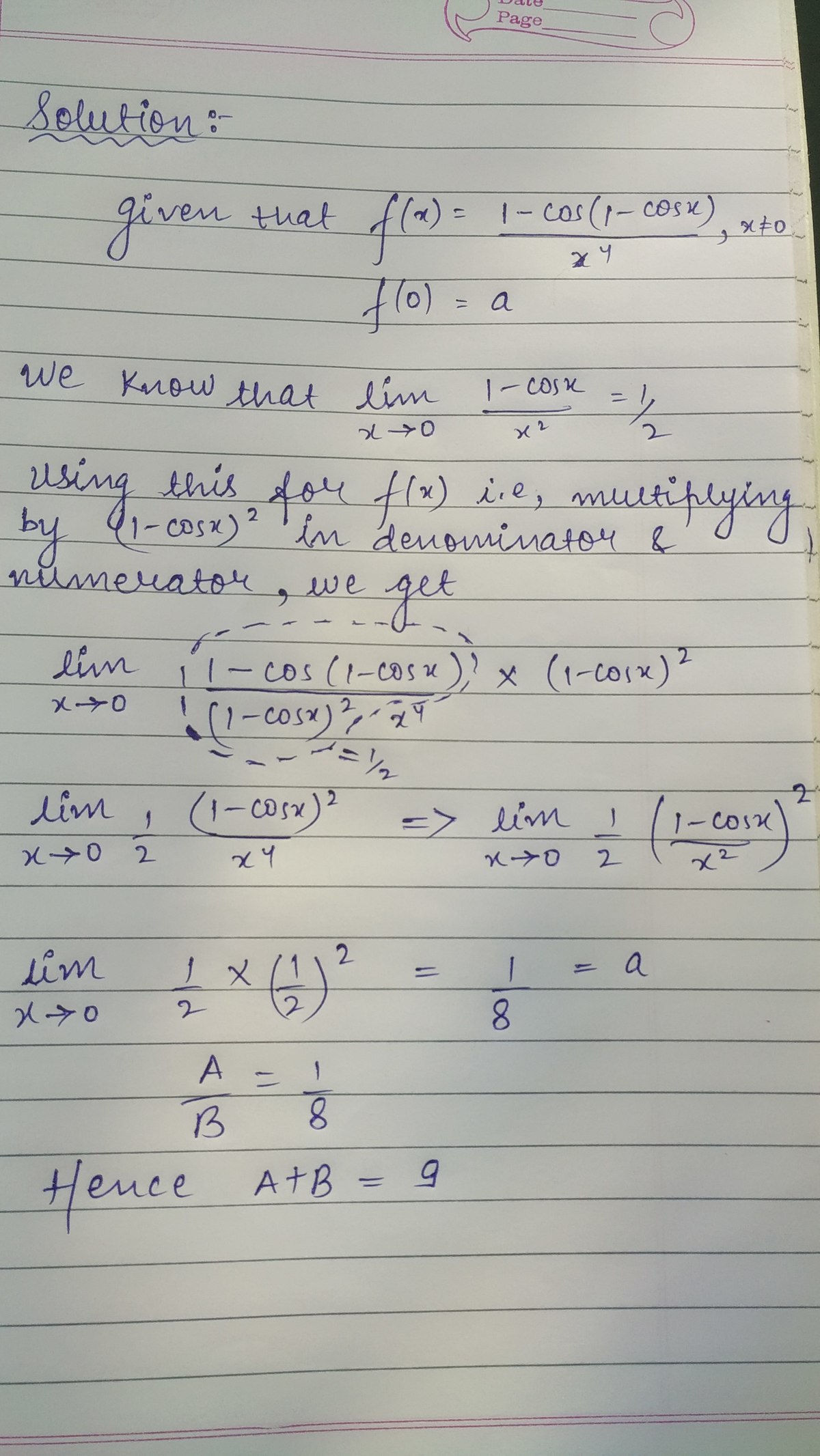
Very nice approach! Great calligraphy too! ^_^

Pi Han Goh - 5 years, 11 months ago

Pi Han Goh
Jun 30, 2015

Here's an alternative solution.

For small $x$ ,we have $\cos(x) \approx 1-\frac{x^2}2$ , so $x^4 = (x^2)^2 \approx \left(2(1-\cos(x)) \right)^2$ . So the limit becomes

$\frac14 \lim_{x\to 0} \frac{1 - \cos(1 - \cos(x))}{(1-\cos(x))^2}$

Let $y = 1- \cos(x)$ , then as $x \rightarrow 0, y \rightarrow 0$ .

$\frac14 \lim_{y\to 0} \frac{1 - \cos(y)}{y^2} = \frac14 \lim_{y\to 0} \frac{(y^2/2)}{y^2} = \boxed{\frac18}$

Moderator note:

You need to be really careful with that approximation substitution. There is some work involved in justifying why it can be done.

This is also a nice way. I hadn't thought of it at all. Thanks sir.

Vishwak Srinivasan - 5 years, 11 months ago

Cos the limit is funny

Try my set .

2 solutions

Moderator note:

0 pending reports