Cos this is simple, solve it in 10 seconds!
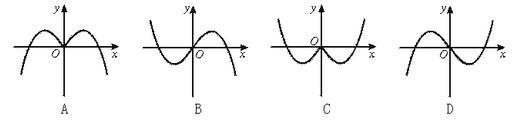
Which is part of the graph of y = − x cos x ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
When you zoom in close to zero, y= -x. (d) is the only one with this behavior.
Since there are options given., my solution is going to be very short.
When 2 − π < x < 0 , − x > 0 , cos x > 0
Hence the graph where the y values are < 0 , for x ∈ ( − 2 π , 0 ) , are excluded.
When 0 < x < 2 π , − x < 0 , cos x > 0
Hence the graph where the y values are > 0 , for x ∈ ( 0 , 2 π ) , are excluded.
Option D is all that is left.
So let us analyse the graph.
At x=0, y=0 and all the graphs satisfy this. At x= Π / 2 , y=- Π / 2 cos( Π / 2 ) = 0 and the graphs seems so satisfy this even though the scale is not mentioned. Now for the critical analysis let us take Π / 4 .
At x= Π / 4 , y=- Π / 4 cos( Π / 4 ) = - Π / ( 4 2 ), which is a negative value. so, A and B are eliminated.
Now at x=- Π / 4 , y = Π / 4 cos(- Π / 4 ) = Π / 4 cos( Π / 4 ) as cos(-x) = cos(x).
so y is positive in this case and thus C is eliminated and answer is D. And as it cos is a periodic function, -xcosx will also be periodic.
y = − x cos x is an odd function, so its graph is symmetrical about ( 0 , 0 ) , therefore A and C are impossible.
Furthermore, when x ∈ ( 0 , 2 π ) , y = − x cos x < 0 .