cos(A+B)=cos(A)+cos(B)
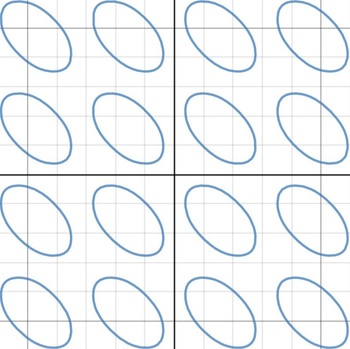
The plot of the equation cos ( x + y ) = cos x + cos y looks like a collection of infinitely many identical closed shapes.
Find the area of one of these closed shapes.
The answer is 15.7373931047.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I assumed the area is elliptical. In that calculation, the area came out to be ≈ 1 5 . 7 4 . Very suspicious!
Log in to reply
Yep, I definitely double-checked using that!
The oval in the transformed coordinates has semi-axes 2 1 ( u 2 − u 1 ) = π − cos − 1 2 1 − 3 , cos − 1 2 − 1 = 3 2 π
so - if we assume it's an ellipse - the area in the original coordinates is 2 π ⋅ ( π − cos − 1 2 1 − 3 ) ⋅ 3 2 π ≈ 1 5 . 7 3 9 5 4 …
which is very, very close.
Let u = 2 1 ( x + y ) and v = 2 1 ( x − y ) . Then the equation becomes cos 2 u = 2 cos u ⋅ cos v and the graph ( v plotted against u ) looks like this: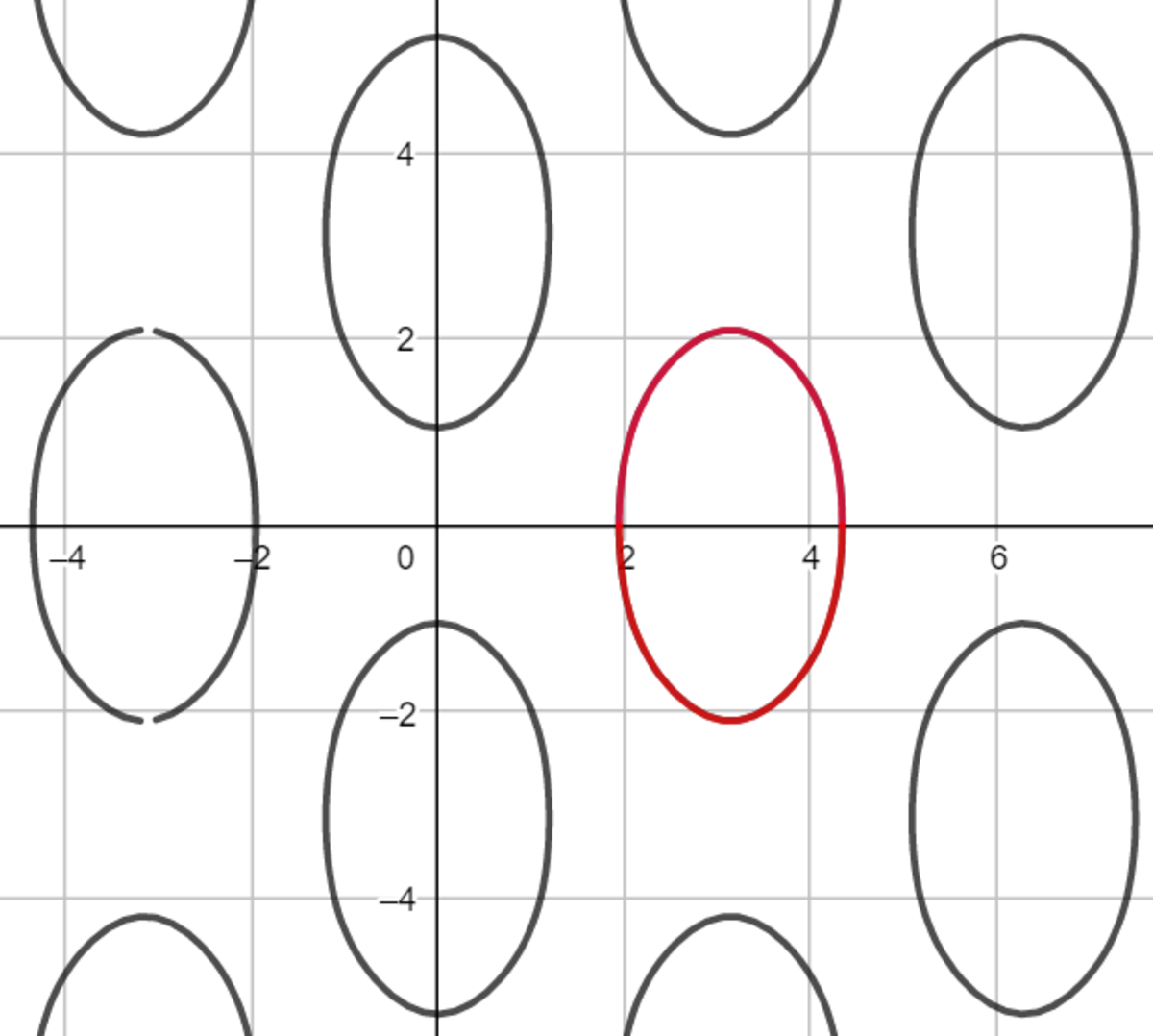
(image produced with GeoGebra)
Due to the transformation of coordinates, the symmetry axes of the ovals are now horizontal/vertical, but the areas have shrunk by a factor of 2 .
We'll concentrate on the oval highlighted in red. To find the intersections of this oval with the u -axis, we need to solve for when v = 0 , ie solve cos 2 u = 2 cos u
This is just a quadratic in cos u ; solving, we find the two intersections are given by u 1 = cos − 1 2 1 − 3 , u 2 = 2 π − u 1
Recalling that areas have been shrunk in these coordinates, and noting that the integral will just give the area of the top half of the oval, the area of one of the shapes in the original coordinates is given by A = 4 ∫ u 1 u 2 cos − 1 ( 2 cos u cos 2 u ) d u
Using Wolfram|Alpha, this came out be 1 5 . 7 3 7 … . (I'd love to see a way to evaluate the integral analytically!)