Cosine and few friends
∫ − 2 0 1 6 π 2 0 1 5 π ( cos ( x ) + ∣ cos ( x ) ∣ + cos ( ∣ x ∣ ) ) d x = ?
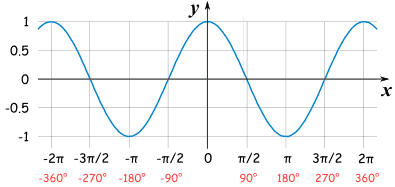
Try also:
Graph credit: Math is Fun
The answer is 8062.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 Let
I
=
∫
−
2
0
1
6
π
2
0
1
5
π
cos
x
+
∣
cos
x
∣
+
cos
∣
x
∣
d
x
=
I
1
+
I
2
+
I
3
respectively.
Let
I
=
∫
−
2
0
1
6
π
2
0
1
5
π
cos
x
+
∣
cos
x
∣
+
cos
∣
x
∣
d
x
=
I
1
+
I
2
+
I
3
respectively.
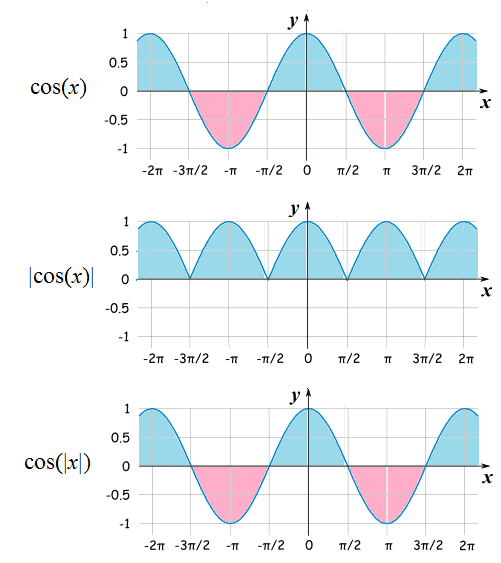
We note that c o s x is an even function with a period or cycle of 2 π and that I c = ∫ a b cos x d x = 0 , when b − a = n π , where n is an integer. Then we have:
I 1 = ∫ − 2 0 1 6 π 2 0 1 5 π cos x d x = 0 Since b − a = 4 0 3 1 π
I 2 = ∫ − 2 0 1 6 π 2 0 1 5 π ∣ cos x ∣ d x = ( 2 0 1 5 − ( − 2 0 1 6 ) ) × 2 ∫ 0 2 π cos x d x = 8 0 6 2 sin x ∣ ∣ ∣ ∣ 0 2 π = 8 0 6 2 All half-cycles are positive.
I 1 = ∫ − 2 0 1 6 π 2 0 1 5 π cos ∣ x ∣ d x = 0 = ∫ − 2 0 1 6 π 2 0 1 5 π cos x d x = 0 Note that cos ∣ x ∣ = cos x as both are even Since b − a = 4 0 3 1 π
Therefore, I = I 1 + I 2 + I 3 = 0 + 8 0 6 2 + 0 = 8 0 6 2 .
∫ − 2 0 1 6 π 2 0 1 5 π ( cos ( x ) + ∣ cos ( x ) ∣ + cos ( ∣ x ∣ ) ) d x = ∫ − 2 0 1 6 π 2 0 1 5 π cos ( x ) d x + ∫ − 2 0 1 6 π 2 0 1 5 π ∣ cos ( x ) ∣ d x + ∫ − 2 0 1 6 π 2 0 1 5 π cos ( ∣ x ∣ ) d x = [ sin ( x ) ] − 2 0 1 6 π 2 0 1 5 π + ∫ − 2 0 1 5 . 5 π 2 0 1 5 . 5 π ∣ cos ( x ) ∣ d x + ∫ 0 2 0 1 5 π cos ( x ) d x + ∫ 0 2 0 1 6 π cos ( x ) d x = [ sin ( x ) ] 0 2 0 1 5 π + [ sin ( x ) ] 0 2 0 1 6 π + 8 0 6 2 ∫ 0 2 1 π cos ( x ) d x = 8 0 6 2