Cosine and Something Else
Let n be a positive nonzero integer and
k
=
4
n
,
a
=
x
+
x
2
−
k
2
,
b
=
x
−
x
2
−
k
2
,
f
(
x
)
=
2
1
k
k
1
(
a
k
+
b
k
)
.
For what integer n < 1 0 0 0 does f ( x ) intersect cos ( x ) the most times between − 4 π < x < 4 π ?
You may want to use a graphing calculator.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
But values of x less than k (in magnitude) do not lie in the domain of the function.
Log in to reply
For k=4n, where n is an integer, complex quantities vanish, and we're left with real numbers, so x < k are in the domain. f(x) always produces a finite polynomial with rational coefficients.
Hi Michael , Can you please look into my post???
Log in to reply
I am unable to understand the mistake in mine..
I am able to prove that both the curves never meet and it also seems to be correct. Don't really know where I have did any mistake in the proof. Kindly go through it and comment on it....
I am new to this site and didn't get accquainted with formatting stuff.... Sorry for that
Given k= 4n
and clearly x^2 > k^2
LHS = (1/2)*((a/k)^k + (b/k)^k)
(a/k)^k * (b/k)^k = 1
and both are positive numbers as K is an even number
So by AM>=GM
we have LHS >=1
RHS = cos(x)
RHS<=1
So this condition satisfies when LHS = RHS =1
LHS = 1 => a=b=x=+/- k
so we have X = +/- K when both the curves meet
and cos(x) = 1
=> x = 2mPi or -(2m+1)Pi
Case 1 : X= 2mPi
=> X=K as K cannot be negative
=> 2mPi = K
=> Pi = K/(2m)
But we know Pi is an irrational number and cannot be expressed as m/n
Similarly for Case also
Case 2: X= -(2m+1)Pi => X=-K
=>K = (2m+1)Pi
Here also Pi condraticts the rules of irrationality
So we can say that both the curves never meet........
No, it's not true that x^2 > k^2. As I pointed out in my reply to Aalap, when expanded, f(x) becomes a polynomial of finite order and with rational coefficients, with a real value even when x^2 < k^2. Your proof depends on that x^2 > k^2 always has to be true.
Log in to reply
Great!!! I am unnecessarily assuming 'a' and 'b' have to be rational..... Thanks for the reply
first check that needs to be done is to see if f(x) is real for all values of x & k. We can see that for that
x 2 − k 2 ≥ 0
Checking this condition we get
x 2 − k 2 ≥ 0 x 2 − k 2 ≥ 0 ( x − k ) ( x + k ) ≥ 0 − x ≤ k ≤ x x v a r i e s f r o m − 4 π t o + 4 π h e n c e − 4 π ≤ k ≤ 4 π n o w k = 4 n s o − 4 π ≤ 4 n ≤ 4 π g i v e s − π ≤ n ≤ π S i n c e n i s a n i n t e g e r < 1 0 0 0 s o t h e o n l y p o s s i b l e v a l u e s o f n c a n b e 1 , 2 , 3 f o r n = 1 f ( x ) = ( 2 1 4 4 1 ) . ( ( x + x 2 − 1 6 ) 4 + ( x − x 2 − 1 6 ) 4 a g a i n w e c a n s e e t h a t x ≥ 4 o r x ≤ − 4 f o r x = 4 f ( x ) = 1 f o r x > 4 o r x < − 4 f ( x ) > 1 t h u s f ( x ) c a n i n t e r s e c t c o s ( x ) a t o n l y x = 4 = 1 . 2 7 2 π c o s ( x ) l i e s b e t w e e n − 1 t o 0 f o r π t o 1 . 5 π . H e n c e n = 1 i s n o t a s o l u t i o n S i m i l a r l y n = 2 & n = 3 i s c h e c k e d . f o r n = 2 x = 2 . 5 4 π ; c o s ( x ) l i e s b e t w e e n 0 & − 1 f o r 2 . 5 π t o 3 π f o r n = 3 x = 3 . 8 2 π ; c o s ( x ) l i e s b e t w e e n 0 & 1 f o r 3 . 5 π t o 4 π T h u s t h e r e i s o n l y o n e s o l u t i o n n = 3
The solution has been found using elimination method. A detailed way wold be to plot the equations. However elimination method is quite useful to narrow down the possible solutions.
Given that k = 4 n for postive integer n , we have
a = x + x 2 − k 2 = x + i k 2 − x 2 = k ( k x + i 1 − ( k x ) 2 )
b = x − x 2 − k 2 = x − i k 2 − x 2 = k ( k x − i 1 − ( k x ) 2 )
We then take advantage of this trigonometric identity
i A r c S i n ( x ) = L o g ( i x + 1 − x 2 )
to rewrite a , b as
a = k i e − i ϕ
b = − k i e i ϕ
where
ϕ = A r c S i n ( k x )
Given that a b = k 2 and plugging in the expressions for a , b , we end up with
2 1 k k 1 ( a k + b k ) = 2 1 ( ( b a ) 2 1 k + ( a b ) 2 1 k ) = 2 1 ( e − i k ϕ + e i k ϕ )
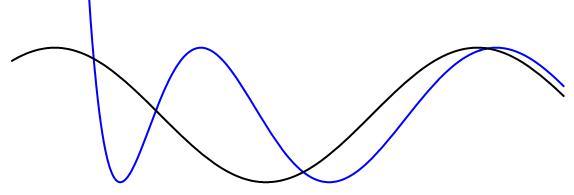
which, as k → ∞ , becomes the exponential expression for C o s ( x ) . Keep in mind that k = 4 n , which eliminates pesky sign problems. Thus, as n increases, it approaches the Cosine function, and from n = 4 on, it never crosses the Cosine function more than 4 times between 0 < x < 4 π . For n = 3 , it crosses the Cosine function 5 times between 0 < x < 4 π . Both functions are symmetric functions of x .
Here's the graphic for n = 6 , the green vertical line is where x = 4 π