Cosine Filter
An 8-tap "cosine filter" takes in a discrete signal x as an input, and produces a discrete output signal y . The filter is designed to pass through 6 0 Hz with unity gain, while rejecting low frequencies and higher integer multiples of 6 0 Hz (see diagram).
If the filter is fed a pure sinusoid as an input, the filter gain is the ratio of the peak value of the output sinusoid to the peak value of the input sinusoid.
The filter is implemented as follows:
y k = Σ n = 0 n = 7 α n x k − n α n = 4 1 c o s ( 8 2 π ( n + 1 / 2 ) )
In the above equations, subscript k denotes the present processing interval, and subscript k − n represents various past processing intervals.
Let the applied frequency in Hz be f , and let the filter gain as a function of frequency be H ( f ) . Determine the following integral, and give your answer as ⌊ I ⌋
I = ∫ 0 3 0 0 H ( f ) d f
Details and Assumptions: The filter is processed at a rate of 4 8 0 samples per second
Hint: Use the time-shift property of the z-transform to derive a transfer function in the z-domain
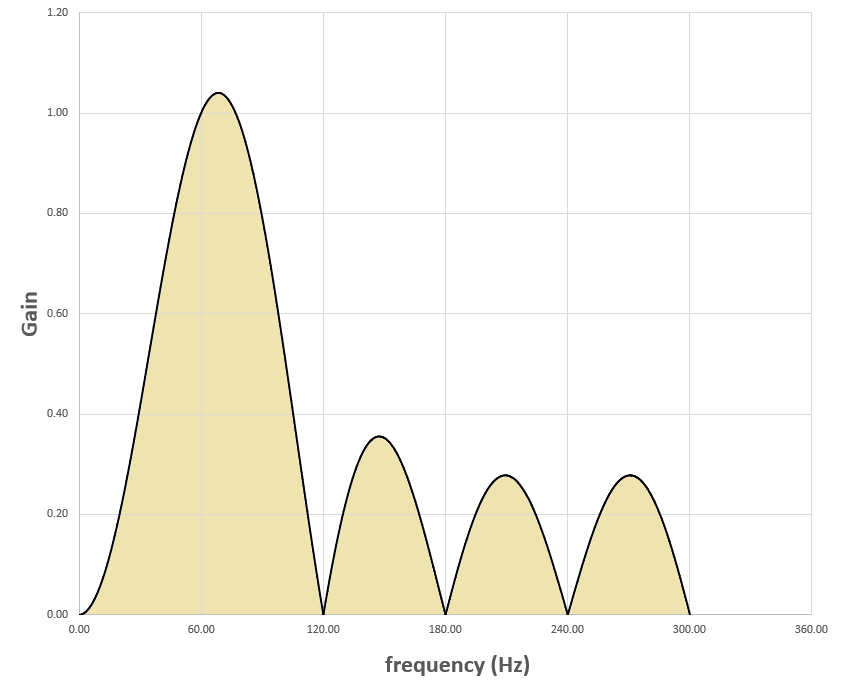
The answer is 103.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very nice solution, thanks
Log in to reply
Thank you, Mr Chase. It's an honor. I always enjoy your problems.
The convolution integral is
y ( k ) = n = 0 ∑ 7 h ( n ) x ( k − n ) ( 1 )
where h ( n ) is the impulse response of the filter, and is referred to in the problem as α n .
If we plug in a complex sinusoidal input of frequency f , as our input, then
x ( k ) = e j 2 π f k ( 2 )
Plugging in (2) into (1) results in
y ( k ) = n = 0 ∑ 7 h ( n ) e j 2 p i f ( k − n ) = e j 2 π f k ( n = 0 ∑ 7 h ( n ) e − j 2 π f n ) ( 3 )
The term between parantheses in (3) is exactly the complex transfer function (The fourier transform of h ( n ) ). That is,
H ( f ) = n = 0 ∑ 7 h ( n ) e − j 2 p i f n ( 4 )
Hence, we can evaluate ∣ H ( f ) ∣ , the magnitude of H ( f ) at each frequency f .
What remains is to numerically integrate that over the range of f from 0 to 3 0 0 H z .
We have:
y ( k ) = n = 0 ∑ 7 4 1 cos [ 8 2 π ( n + 1 / 2 ) ] x ( k − n )
Using the referred time-shift property and considering that x ( k ) = 0 for k ≤ 0 , i.e., assuming the time begins to count when the signal begins, and denoting X ( z ) and Y ( z ) as the Z-transforms of x ( k ) and y ( k ) respectively:
Y ( z ) = X ( z ) ⋅ ⎣ ⎡ n = 0 ∑ 7 4 1 cos [ 8 2 π ( n + 1 / 2 ) ] z − n ⎦ ⎤
The transfer function T ( z ) is the ratio between output and input:
T ( z ) = 4 1 ⎣ ⎡ n = 0 ∑ 7 cos [ 8 2 π ( n + 1 / 2 ) ] z − n ⎦ ⎤
Since we're sampling at 4 8 0 Hz, to convert from Z-transform to Laplace Transform we make z = e s ⋅ T s , where T s is the sampling period:
T ( s ) = 4 1 ⎣ ⎡ n = 0 ∑ 7 cos [ 8 2 π ( n + 1 / 2 ) ] e − 4 8 0 s ⋅ n ⎦ ⎤
In the time domain, if we input a signal x ( t ) through a transfer function p ( t ) , the output signal y ( t ) is a convolution, i.e.:
y ( t ) = ∫ 0 ∞ p ( τ ) x ( t − τ ) d τ
If x happens to be a sinusoid, i.e., a signal in the form e j ω t ( j is the imaginary unit) or a linear combination of such signals (recall that cosine and sine are indeed linear combinations of signals like this), then we have:
y ( t ) = ∫ 0 ∞ p ( τ ) e j ω ( t − τ ) d τ
y ( t ) = e j ω t ∫ 0 ∞ p ( τ ) e − j ω τ d τ
This integral is the exact definition of Laplace transform of p ( t ) (denoted P ( s ) ) evaluated at s = j ω (also known as Fourier Transform ):
y ( t ) = e j ω t P ( j ω )
This means that if we input a sinusoid with frequency ω through a transfer function p ( t ) , it will receive a gain equal to the absolute value of P ( j ω ) and a phase change equal to the angle of P ( j ω ) .
So, the gain at linear frequency f (angular frequency 2 π f ) is equal to the absolute value of T ( j 2 π f ) . Thus:
H ( f ) = ∣ T ( j 2 π f ) ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 4 1 ⎣ ⎡ n = 0 ∑ 7 cos [ 8 2 π ( n + 1 / 2 ) ] e − 4 8 0 n ⋅ j 2 π f ⎦ ⎤ ∣ ∣ ∣ ∣ ∣ ∣
Integrating it numerically from f = 0 to 3 0 0 gives:
I = ∫ 0 3 0 0 H ( f ) d f ≈ 1 0 3 . 0 6 4 → ⌊ I ⌋ = 1 0 3