Cotangent Rule

Geometry Level pending

If $x$ , $y$ and $z$ are different angles of a triangle. What the value of:

$\cot(x)\cot(y)+\cot(y)\cot(z)+\cot(x)\cot(z)?$

The answer is 1.

2 solutions

Ahmad Saad
Apr 18, 2017

@DSCAS G , this problem is quite easy as an mcq question by just taking the triangle as equilateral.

So its best at subjective question

Md Zuhair - 4 years, 1 month ago

Chew-Seong Cheong
Apr 18, 2017

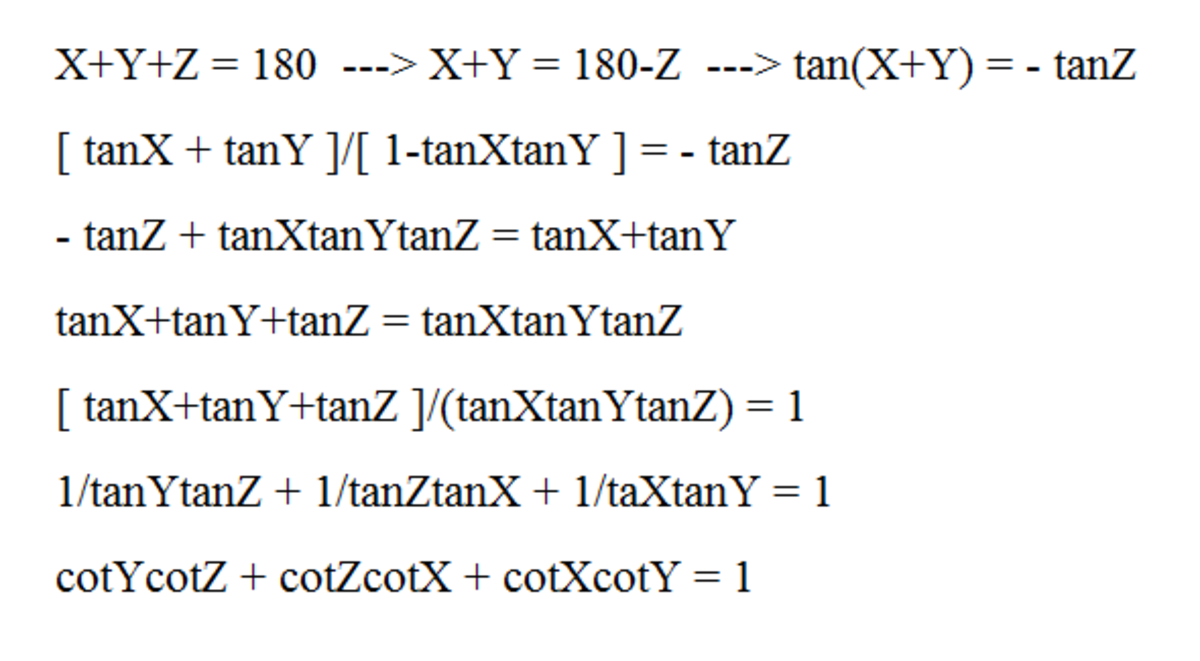
If $x$ , $y$ and $z$ are angles of a triangle, then:

$\begin{aligned} \tan x + \tan y + \tan z & = \tan x \tan y \tan z & \small \color{#3D99F6} \text{Dividing both sides by } \tan x \tan y \tan z \\ \frac {\tan x}{\tan x \tan y \tan z } + \frac {\tan y}{\tan x \tan y \tan z } + \frac {\tan z}{\tan x \tan y \tan z } & = 1 \\ \frac 1{\tan y \tan z } + \frac 1{\tan x \tan z } + \frac 1{\tan x \tan y} & = 1 \\ \cot y \cot z + \cot x \cot z + \cot x \cot y & = \boxed{1} \end{aligned}$

Don't you think the triangle should be non - oblique for the solution to be legitimate ?

Aditya Sky - 4 years, 1 month ago

$\tan x + \tan y + \tan z = \tan x \tan y \tan z$ is true for all triangles.

Chew-Seong Cheong - 4 years, 1 month ago

That's true. What I'm saying is that if the triangle is oblique, then one of the $\tan(A)$ , $\tan(B)$ or $\tan(C)$ would be undefined, in which case you can't divide the equation by $\tan(A) \cdot tan(B) \cdot tan(C)$ .

Aditya Sky - 4 years, 1 month ago

I don't get you. $\tan \theta \in (-\infty, \infty)$ for $\theta \in (0,\pi)$ , which angle is undefined? Just suggest three valid angles to disprove it, if you can. Of course, angle of a real triangle cannot be larger than $\pi$ .

Chew-Seong Cheong - 4 years, 1 month ago

Cotangent Rule

The answer is 1.

2 solutions

0 pending reports