Couette Flow

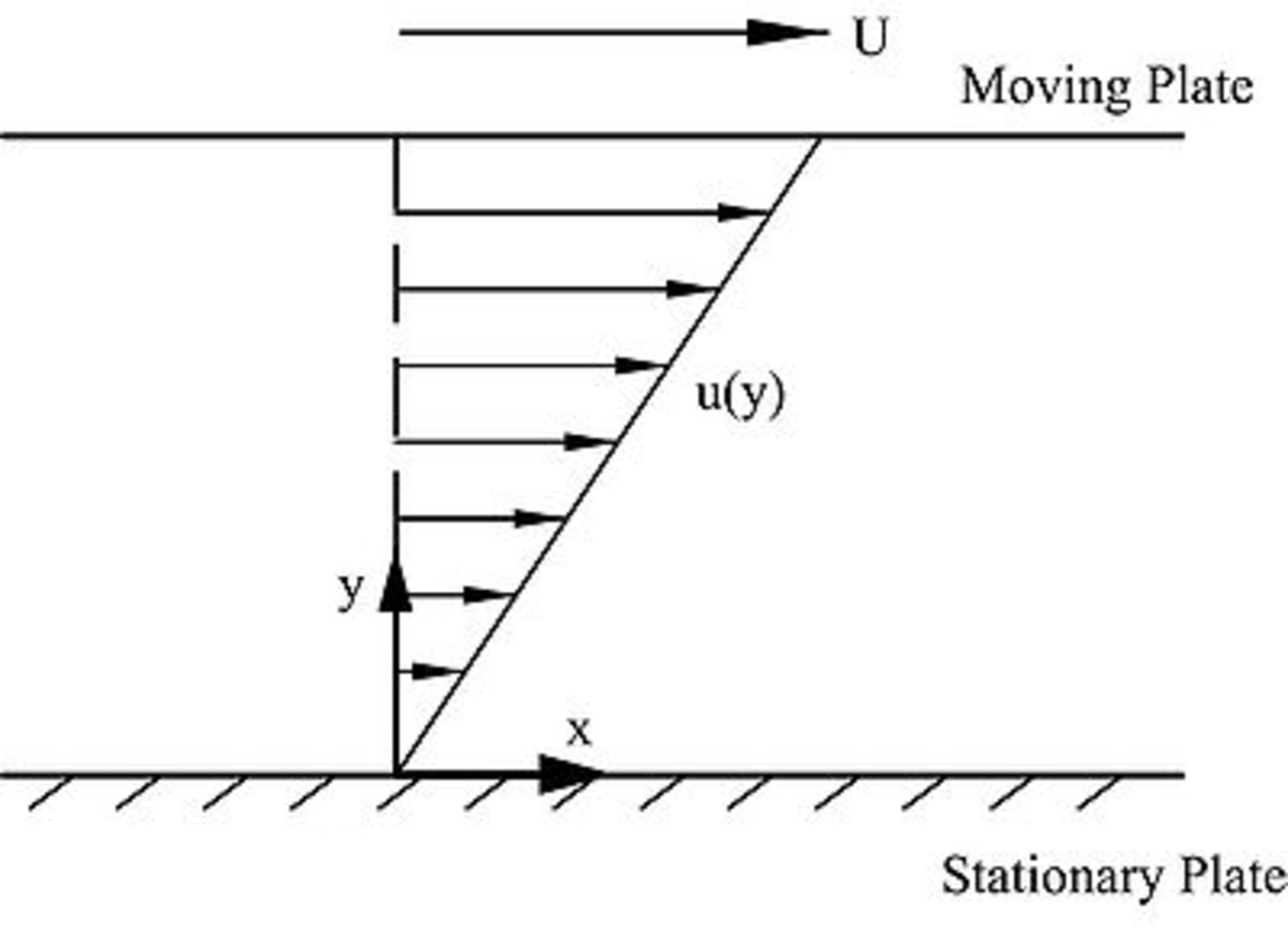
The flow between two parallel plates, with the upper plate moving with constant velocity $U$ and distance $h$ between them, can be described by the differential equation below: $\frac{d^2 u}{dy^2} =0,$ where $u$ is the flow velocity and $y$ is the distance from the lower plate. Considering that the distance between the plates is $h = 1$ mm and that the upper plate is moving with constant speed $U = 1$ m/s, which is the expression for the flow velocity $u(y)$ as a function of $y$ ?