Coulomb vs Newton and the battle of the inverse square force laws

Electricity and Magnetism Level 3

The laws of nature seem to prefer inverse square force field laws. Where the strength of a field of force decays as 1 r 2 \frac{1}{{{r}^{2}}} the separation distance between the source and the object. These laws include Newton’s law of gravity and law of electricity and magnetism. Newton's law of gravity states that the gravitational force of mass 1 ( m 1 {{m}_{1}} ) on mass 2 ( m 2 {{m}_{2}} ) and vice versa, is proportional to the gravitation constant G and the product of their masses and inversely proportional to the square of their distance between them or mathematically written as F G = G m 1 ⋅ m 2 r 2 {{F}_{G}}=G\frac{{{m}_{1}}\cdot {{m}_{2}}}{{{r}^{2}}} , where G = 6.674 × 10 − 11 N ⋅ m 2 k g 2 G=6.674\times {{10}^{-11}}\frac{N\cdot {{m}^{2}}}{k{{g}^{2}}} . This is the law that tells the heavenly bodies how to move and apples, here on earth, how to fall. It is purely an attractive force and is pulling everything toward the center. But there is another inverse square law for charges (like electrons, protons, ions, and the like) called Coulomb's law. And the Coulomb force between two charges is proportional to the product of their charges and inversely proportional their separation distance, mathematically written as F C = 1 4 π ε 0 q 1 ⋅ q 2 r 2 {{F}_{C}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{r}^{2}}} , where ε 0 = 8.85 × 10 − 12 C 2 N ⋅ m 2 {{\varepsilon }_{0}}=8.85\times {{10}^{-12}}\frac{{{C}^{2}}}{N\cdot {{m}^{2}}} . This law is both attractive and repulsive, where like charges repulsive each other and unlike charges attract each other. What we want to know is what is the relative strengths between these forces, defined as α = F C F G \alpha =\frac{{{F}_{C}}}{{{F}_{G}}} ?

So, let us say you jump and land on your feet. Now, the question is, why don’t you fall to the center of the earth? According to the gravitational force, this should pull you towards the earth’s center, but obviously, this does not happen. The answer here lies in the repulsive forces between the electrons in your feet and the ground. But, how much stronger is the Coulomb force to the gravitational force between the two electrons, given that charge is e = 1.602 × 10 − 19 C e=1.602\times {{10}^{-19}}C and mass m e = 9.11 × 10 − 31 k g {{m}_{e}}=9.11\times {{10}^{-31}}kg or what is the value for α \alpha (if your answer is 1.23 × 1 0 4 1.23\times 10^4 submit 1.23E4)?


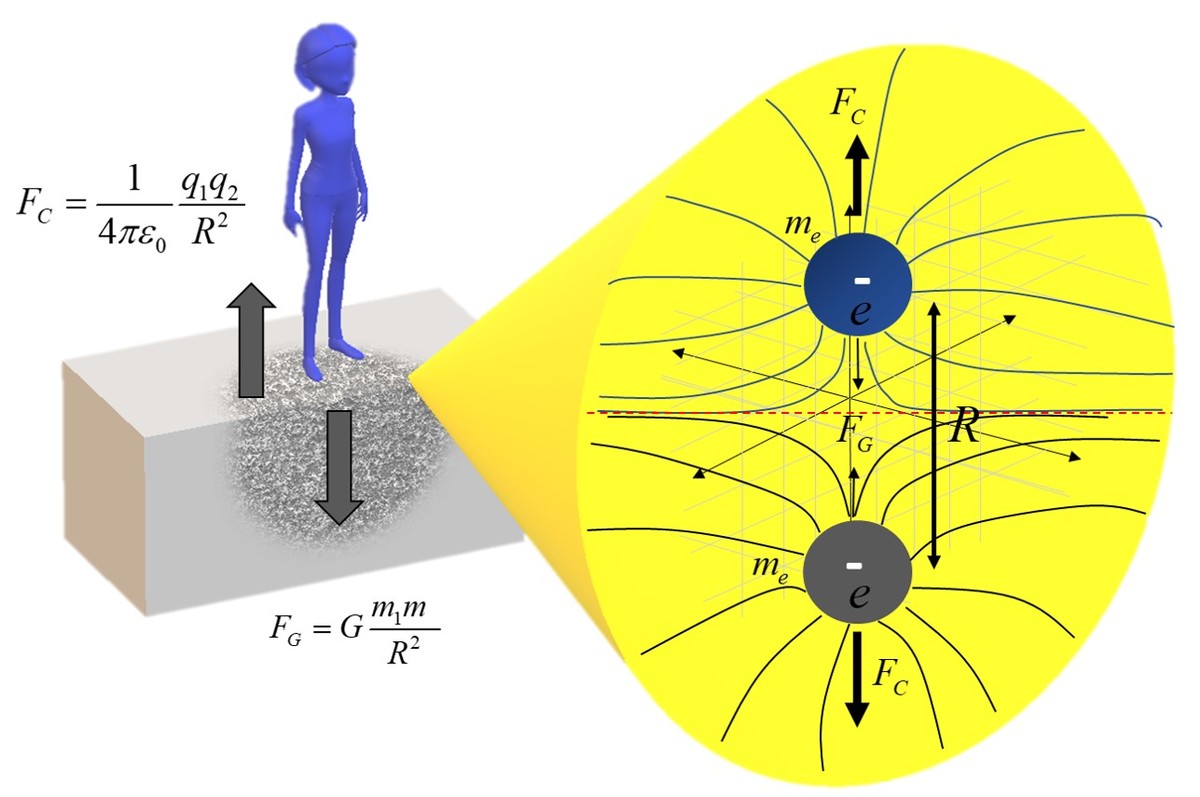
The answer is 4.16E+42.

Bradley Nordell by Bradley Nordell , 34, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Bradley Nordell
Jun 22, 2018

α = F C F G = ( 1 4 π ε 0 ) ( e 2 r 2 ) G ( m e 2 r 2 ) = ( e 2 4 π ε 0 ) G ⋅ m e 2 = ( ( 1.602 × 10 − 19 C ) 2 4 π ⋅ 8.854 × 10 − 12 C 2 N ⋅ m 2 ) 6.674 × 10 − 11 N m 2 k g ⋅ ( 9.11 × 10 − 31 k g ) 2 = 4.2 × 10 42 \alpha =\frac{{{F}_{C}}}{{{F}_{G}}}=\frac{\left( \frac{1}{4\pi {{\varepsilon }_{0}}} \right)\left( \frac{{{e}^{2}}}{{{r}^{2}}} \right)}{G\left( \frac{m_{e}^{2}}{{{r}^{2}}} \right)}=\frac{\left( \frac{{{e}^{2}}}{4\pi {{\varepsilon }_{0}}} \right)}{G\cdot m_{e}^{2}}=\frac{\left( \frac{{{\left( 1.602\times {{10}^{-19}}C \right)}^{2}}}{4\pi \cdot 8.854\times {{10}^{-12}}\frac{{{C}^{2}}}{N\cdot {{m}^{2}}}} \right)}{6.674\times {{10}^{-11}}\frac{N{{m}^{2}}}{k{{g}^{{}}}}\cdot {{\left( 9.11\times {{10}^{-31}}kg \right)}^{2}}}=4.2\times {{10}^{42}}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...