Count a factorial

Computer Science Level 3

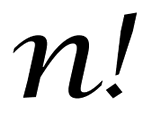
A factorial number $F$ is any natural number for $n>0$ such that $F=n!$ . So the first few factorial numbers are $1, 2, 6, 24, 120, 720 ......$ . Implement an algorithm that takes two parameters (low, high) and returns the count of the factorial number in that range. How many factorial numbers are there between $10^{13}$ and $10^{1000}$

The answer is 434.

2 solutions

Hasmik Garyaka
Oct 11, 2017

```Python```
def stirling(n):
    return math.log10(math.sqrt(2*n*math.pi))+n*math.log10(n/math.e)

i=1
while stirling(i)<13:i+=1
low=i

while stirling(i)<1000:i+=1
high=i

print(high-low)

Eamon Gupta
Aug 17, 2015

I'm still a beginner in programming so there are probably shorter solutions but here is my code in Python 2.7:

import math

def CountFact(low, high):
    x=1
    count = 0
    while math.factorial(x)<low:
        x+=1
    while math.factorial(x)>low and math.factorial(x)<high:
        count+=1
        x+=1
    if math.factorial(x)>high:
        return count

Line 6 starts with x = 0 , and adds 1 until x! > low. When the value of x! is between low and high, the counter counts how many values of x satisfy the condition while incrementing x. And when x!>high, the count is printed.

Moderator note:

That's a good solution for a beginner! It's great that you explained why your code works :)

A better and efficient way to do this is to make use of logarithms. We know that $f(x)=\log_{10}x$ and $g(x)=10^x$ are strictly increasing functions $\forall~x\in (0,\infty)$ , so we can apply logarithm of base $10$ to all sides of an inequality and the inequality direction remains preserved. Similarly, we can apply exponential of base $10$ to all sides of an inequality and the inequality direction remains preserved. So, we have,

$\textrm{low}\lt n!\lt \textrm{high}\iff \log_{10}(\textrm{low})\lt \log_{10}(n!)=\sum_{k=1}^n\log_{10}k\lt \log_{10}(\textrm{high})$

So, we can use the latter equivalent condition to implement an algorithm to get the count of the factorials between low and high . The advantage of this method is that it's computationally more efficient since it avoids computing large values of factorials. Also, this algorithm is portable to other languages which do not support such big value storing native datatype (for example, C++).

Here 's a C++ code using this algorithm. I can't take the low and high as parameters since there's no native C++ datatype to store such large parameters. Instead I #define d the base $10$ logarithms of low and high as LOW_LOG_10 and HIGH_LOG_10 for this problem at the beginning manually. To change the parameters, you'll need to manually fork the code and change the values of LOW_LOG_10 and HIGH_LOG_10 by redefining them accordingly.

Prasun Biswas - 5 years, 9 months ago

Count a factorial

The answer is 434.

2 solutions

Moderator note:

0 pending reports