Count 'em All 11!
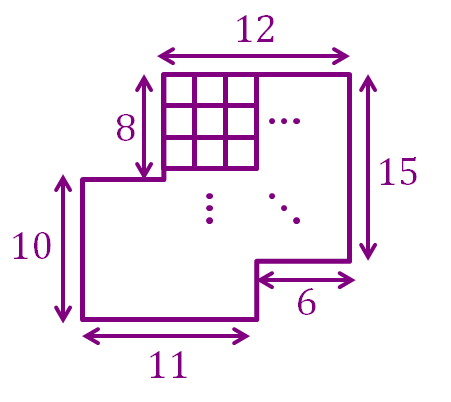
Count the total number of quadrilaterals in the irregular grid above.
Clarifications:
- Quadrilateral is a polygon that has 4 sides.
This is one part of Quadrilatorics .
The answer is 13746.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's fill in the holes so that it becomes a perfectly rectangular grid.
From this note , we know that the number of quadrilaterals in a 1 7 × 1 8 grid is ( 2 1 8 ) × ( 2 1 9 ) = 4 1 7 × 1 8 × 1 8 × 1 9 = 2 6 1 6 3
Now we need to remove the quadrilaterals that are not part of the original grid. To do this, let's split it into 3 cases:
This is trivial, all we need to do is first choose the top-left corner in A, there are 5 × 8 = 4 0 ways to do so, then we choose the bottom-right corner in B, there are 6 × 3 = 1 8 ways to do so.
Hence the number of quadrilaterals with its top-left corner in region A and its bottom-right corner in region B is 4 0 × 1 8 = 7 2 0
Suppose we choose the top-left corner of the quadrilateral i units away from the left boundary of the whole grid and j units away from the top boundary of the whole grid.
Then, the number of ways of choosing the bottom-right corner of the quadrilateral (excluding those lying in region B) is ( 1 7 − i ) ( 1 8 − j ) − 6 × 3 .
Thus, the total number of quadrilaterals with its top-left corner in region A but its bottom-right corner not in region B is j = 0 ∑ 7 i = 0 ∑ 4 [ ( 1 7 − i ) ( 1 8 − j ) − 1 8 ] = j = 0 ∑ 7 i = 0 ∑ 4 [ ( j − 1 8 ) i − 1 7 j + 2 8 8 ] = j = 0 ∑ 7 [ 2 4 × 5 ( j − 1 8 ) − 5 ( 1 7 j − 2 8 8 ) ] = j = 0 ∑ 7 ( 1 0 j − 1 8 0 − 8 5 j + 1 4 4 0 ) = j = 0 ∑ 7 ( 1 2 6 0 − 7 5 j ) = 7 9 8 0
Similarly, suppose we choose the bottom-right corner of the quadrilateral i units away from the right boundary of the whole grid and j units away from the bottom boundary of the whole grid.
Then, the number of ways of choosing the top-left corner of the quadrilateral (excluding those lying in region A) is ( 1 7 − i ) ( 1 8 − j ) − 5 × 8 .
Thus, the total number of quadrilaterals with its top-left corner not in region A but its bottom-right corner in region B is j = 0 ∑ 2 i = 0 ∑ 5 [ ( 1 7 − i ) ( 1 8 − j ) − 4 0 ] = j = 0 ∑ 2 i = 0 ∑ 5 [ ( j − 1 8 ) i − 1 7 j + 2 6 6 ] = j = 0 ∑ 2 [ 2 5 × 6 ( j − 1 8 ) − 6 ( 1 7 j − 2 6 6 ) ] = j = 0 ∑ 2 ( 1 5 j − 2 7 0 − 1 0 2 j + 1 5 9 6 ) = j = 0 ∑ 2 ( 1 3 2 4 − 8 7 j ) = 3 7 1 7
Therefore, the number of quadrilaterals in the original grid is 2 6 1 6 3 − 7 2 0 − 7 9 8 0 − 3 7 1 7 = 1 3 7 4 6 .