Count 'em All 15!
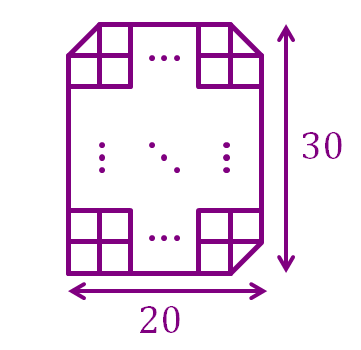
The figure above shows a grid but with 3 of its corners cut off forming triangles.
Count the total number of quadrilaterals in the grid above.
Clarification :
- A quadrilateral is a polygon that has 4 sides.
This is one part of Quadrilatorics .
The answer is 96042.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's pretend the corners aren't cut and the grid is 'perfect'. I'll demonstrate this by patching the 3 cut corners with golden corner squares, and for convenience I'll also label them as A , B , C .
From this note , we know that the number of quadrilaterals in this 'perfect' grid is ( 2 2 1 ) × ( 2 3 1 ) = 4 2 0 × 3 0 × 2 1 × 3 1 = 9 7 6 5 0
But this grid isn't actually perfect, just like how our lives aren't perfect. We need to remove some of the affected quadrilaterals that will no longer be quadrilaterals when the golden corner squares are cut.
If a quadrilateral contains any of the golden corner squares and its width and height are either both bigger than 1 or both equal 1, then this quadrilateral will no longer be a quadrilateral when the golden corners are cut and we need to remove it (if only one of its width or height equals 1 and the other is not, then this quadrilateral will be cut into a trapezium, which is still a quadrilateral).
Let's first count the number of quadrilaterals containing golden corner squares with width and height both equal 1 , this is trivial as that would just be the 3 golden corner squares themselves.
Let's now count the quadrilaterals containing golden corner squares with width and height both bigger than 1 . If we denote n ( □ ) as the number of quadrilaterals with width and height both bigger than 1 which contain at least the specified corners (for example n ( B , C ) would equal to the number of quadrilaterals with width and height both bigger than 1 that contain the corners B , C , which might also contain A ), then by PIE , the total number of desired quadrilaterals is n ( A ) + n ( B ) + n ( C ) − n ( A , B ) − n ( B , C ) − n ( A , C ) + n ( A , B , C )
Consider n ( A ) . Note that we can construct quadrilaterals by choosing 2 squares in the grid as its opposite corner squares, with that in mind, if a quadrilateral's top-left corner square lies on A , then its opposite corner square must not lie on the same row or column as A (since its width and height must be both bigger than 1), and so the number of possible locations for its bottom-right corner square is n ( A ) = ( 2 0 − 1 ) × ( 3 0 − 1 ) = 5 5 1
With similar reasoning, we can also conclude that n ( B ) = n ( C ) = n ( A ) = 5 5 1 .
Consider n ( A , B ) . To construct these quadrilaterals, its top-left corner square must lie on A , and its bottom-right corner square must lie on the same column as B , but not on the same row as A , so the number of possible locations for its bottom-right corner square is n ( A , B ) = 3 0 − 1 = 2 9
Now consider n ( B , C ) . To construct these quadrilaterals, its top-right corner square must lie on B , and its bottom-left corner square must lie on the same row as C , but not on the same column as B , so the number of possible locations for its bottom-left corner square is n ( B , C ) = 2 0 − 1 = 1 9
Lastly let's consider n ( A , C ) and n ( A , B , C ) . It's easy to see that n ( A , C ) = n ( A , B , C ) = 1 .
So, n ( A ) + n ( B ) + n ( C ) − n ( A , B ) − n ( B , C ) − n ( A , C ) + n ( A , B , C ) = 3 × 5 5 1 − 2 9 − 1 9 − 1 + 1 = 1 6 0 5
The total number of quadrilaterals we need to remove is 1 6 0 5 + 3 = 1 6 0 8 , and therefore, the total number of quadrilaterals in the original grid is 9 7 6 5 0 − 1 6 0 8 = 9 6 0 4 2 .