Count 'em Staircases (Count 'em All 16!)
A staircase grid is a grid of squares that resembles a staircase shape. For example, the figure below shows 4 staircase grids with dimensions , , , respectively.
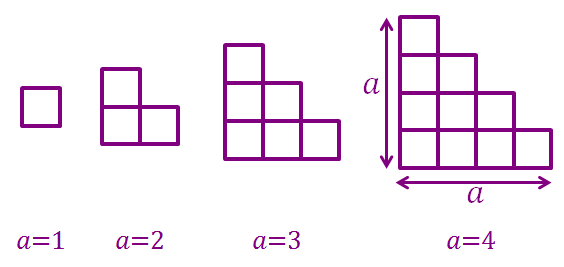
Count the total number of quadrilaterals in a staircase grid (that is, when ).
Clarification:
- A quadrilateral is a polygon that has 4 sides.
This is one part of Quadrilatorics .
The answer is 40920.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose the number of quadrilaterals in an a × a staircase grid is Q a .
Let's try finding Q a + 1 .
As shown in the figure above, to increase a by 1, we simply add a + 1 squares to the hypotenuse (the yellow squares), the newly formed quadrilaterals must contain one of the yellow squares as its top-right corner square.
Let's say we choose one of the yellow squares that is i units away from the left boundary of the new staircase grid as the top-right corner square of the new quadrilateral, then that square must be a − i units away from the bottom boundary of the new staircase grid and the number of possible locations for its bottom-left corner square is ( i + 1 ) ( a − i + 1 ) .
Therefore, Q a + 1 = Q a + i = 0 ∑ a ( i + 1 ) ( a − i + 1 ) = Q a + i = 0 ∑ a ( a i − i 2 + a + 1 ) = Q a + 2 a 2 ( a + 1 ) − 6 a ( a + 1 ) ( 2 a + 1 ) + a 2 + 2 a + 1 = Q a + 6 a 3 + 6 a 2 + 1 1 a + 6
Now we have Q a = Q a − 1 + 6 ( a − 1 ) 3 + 6 ( a − 1 ) 2 + 1 1 ( a − 1 ) + 6 Q a − 1 = Q a − 2 + 6 ( a − 2 ) 3 + 6 ( a − 2 ) 2 + 1 1 ( a − 2 ) + 6 Q a − 2 = Q a − 3 + 6 ( a − 3 ) 3 + 6 ( a − 3 ) 2 + 1 1 ( a − 3 ) + 6 ⋮ Q 3 = Q 2 + 6 2 3 + 6 ( 2 ) 2 + 1 1 ( 2 ) + 6 Q 2 = Q 1 + 6 1 3 + 6 ( 1 ) 2 + 1 1 ( 1 ) + 6
Adding up all of these equations, cancelling out all the like terms and noting that Q 1 = 1 , we have Q a = 1 + 6 [ 2 a ( a − 1 ) ] 2 + a ( a − 1 ) ( 2 a − 1 ) + 2 1 1 a ( a − 1 ) + 6 ( a − 1 ) = 6 a [ 4 a 3 − 2 a 2 + a + 2 a 2 − 3 a + 1 + 2 1 1 a − 1 1 + 6 ] = 2 4 a ( a 3 − 2 a 2 + a + 8 a 2 − 1 2 a + 2 8 + 2 2 a − 2 2 ) = 2 4 a ( a 3 + 6 a 2 + 1 1 a + 6 ) = 2 4 a ( a + 1 ) ( a + 2 ) ( a + 3 )
Finally, substituting a = 3 0 we would get the answer 4 0 9 2 0 .