Count 'em All 22!
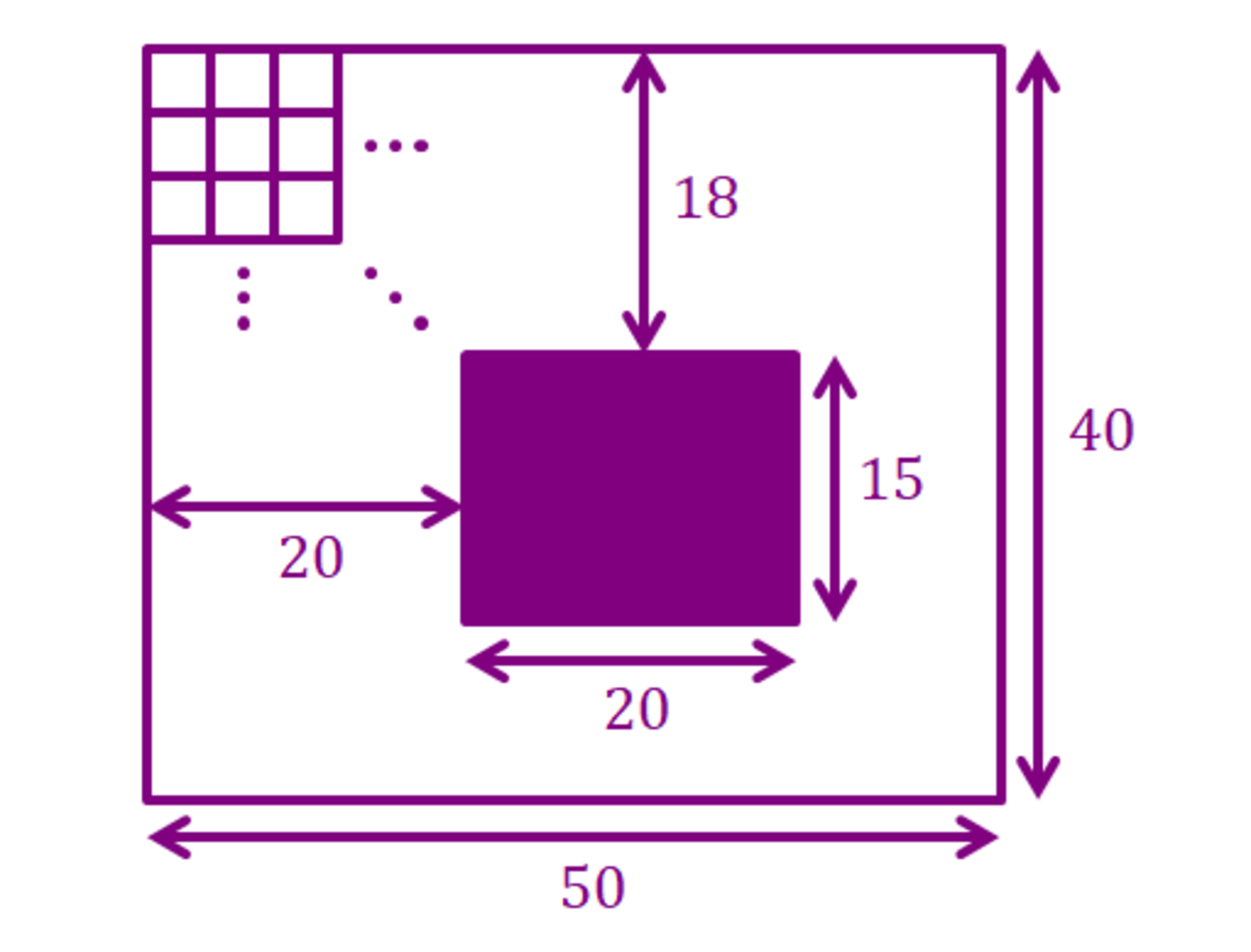
The figure above shows a grid... but this time with a mega giant hole in the middle! How utterly convenient!
Count the total number of quadrilaterals in the grid above.
Clarifications :
- A quadrilateral is a polygon that has 4 sides.
- The quadrilaterals cannot contain the giant hole! I don't like giant holes. :(
- The mouse has gone haywire I think.
This is one part of Quadrilatorics .
The answer is 418290.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Hint:Let the numbers of rectangles in a m × n grid be f ( m , n ) = 4 m n ( m + 1 ) ( n + 1 )
Evaluate f ( 2 0 , 4 0 ) + f ( 1 0 , 4 0 ) + f ( 5 0 , 1 8 ) + f ( 5 0 , 7 ) − f ( 2 0 , 1 8 ) − f ( 2 0 , 7 ) − f ( 1 0 , 1 8 ) − f ( 1 0 , 7 ) and get 4 1 8 2 9 0
a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3
Cut the rectangle into nine areas(notice that b 2 is the hole).
Count the rectangles in "row a ( a 1 ∪ a 2 ∪ a 3 ,the 5 0 × 1 8 rectangle)","row c ","column 1 ","column 3 ".
But we counted the rectangles in a 1 , a 3 , c 1 , c 3 twice,so we have to subtract it.