Count 'em All 6!
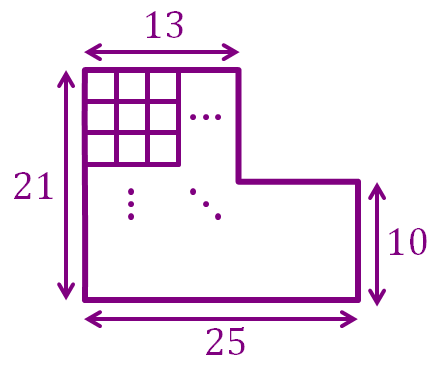
Count the total number of squares in the irregular grid above.
Wait a minute, this looks familiar...
Clarifications:
- Squares are rectangles that have the same width and height, e.g. , , , etc.
This is one part of Quadrilatorics .
The answer is 2207.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We'll divide the grid into 3 parts, A, B and the shaded part: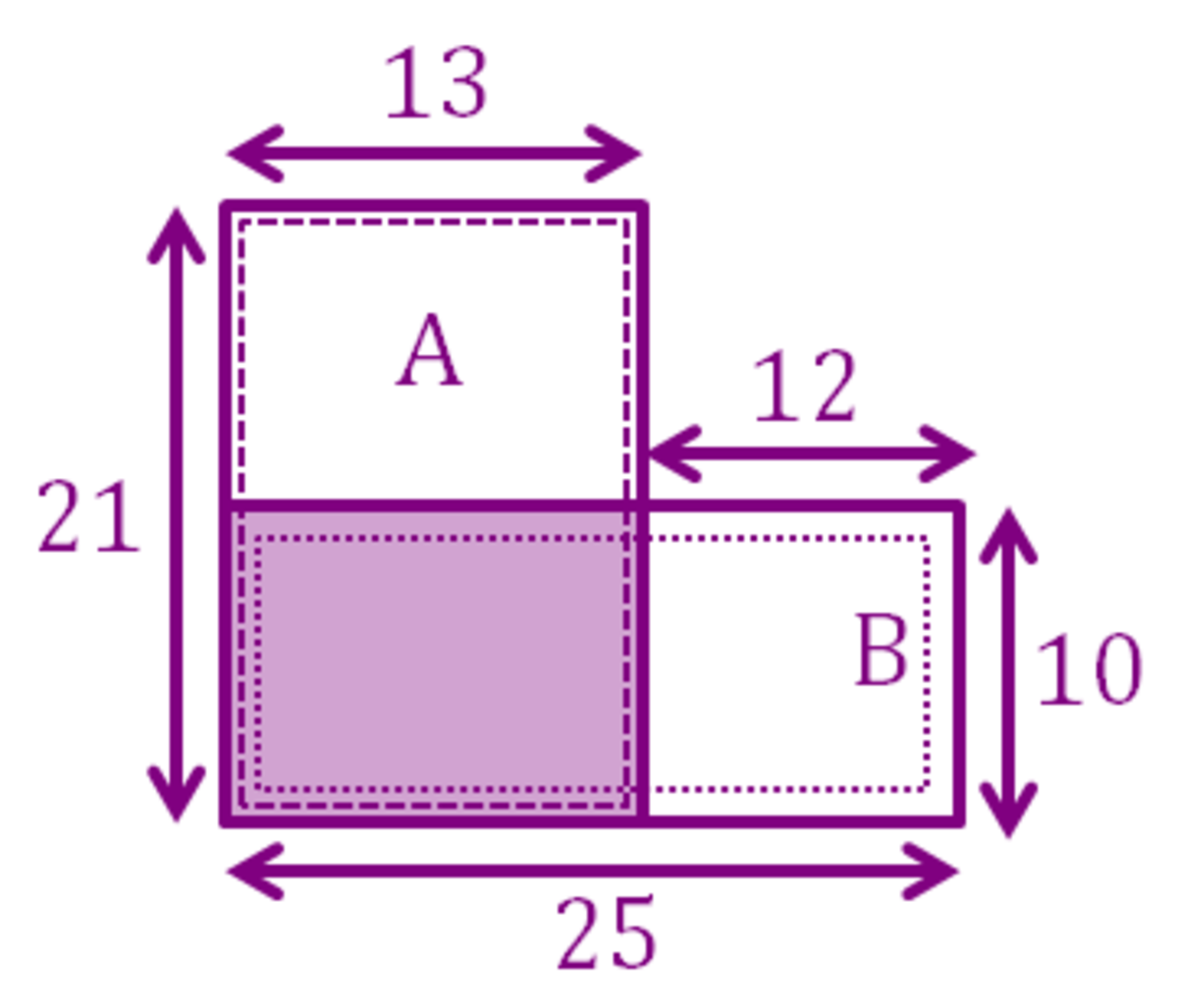 So the number of squares in the original grid is equal to the number of squares in grid A, plus the number of squares in grid B, minus the number of squares in the shaded grid.
So the number of squares in the original grid is equal to the number of squares in grid A, plus the number of squares in grid B, minus the number of squares in the shaded grid.
Using the formula from this note , the number of squares in grid A ( a = 1 3 , b = 2 1 , a is the width of the grid while b is the height of the grid, but since a < b we swap them around so it becomes a = 2 1 , b = 1 3 ) is 6 1 3 × 1 4 × ( 3 × 2 1 − 1 3 + 1 ) = 1 5 4 7
Similarly the number of squares in grid B ( a = 2 5 , b = 1 0 ) is 6 1 0 × 1 1 × ( 3 × 2 5 − 1 0 + 1 ) = 1 2 1 0
The number of squares in the shaded grid ( a = 1 3 , b = 1 0 ) is 6 1 0 × 1 1 × ( 3 × 1 3 − 1 0 + 1 ) = 5 5 0
Hence, the number of squares in the original grid is 1 5 4 7 + 1 2 1 0 − 5 5 0 = 2 2 0 7 .