Count 'em All 8!

Probability Level 3

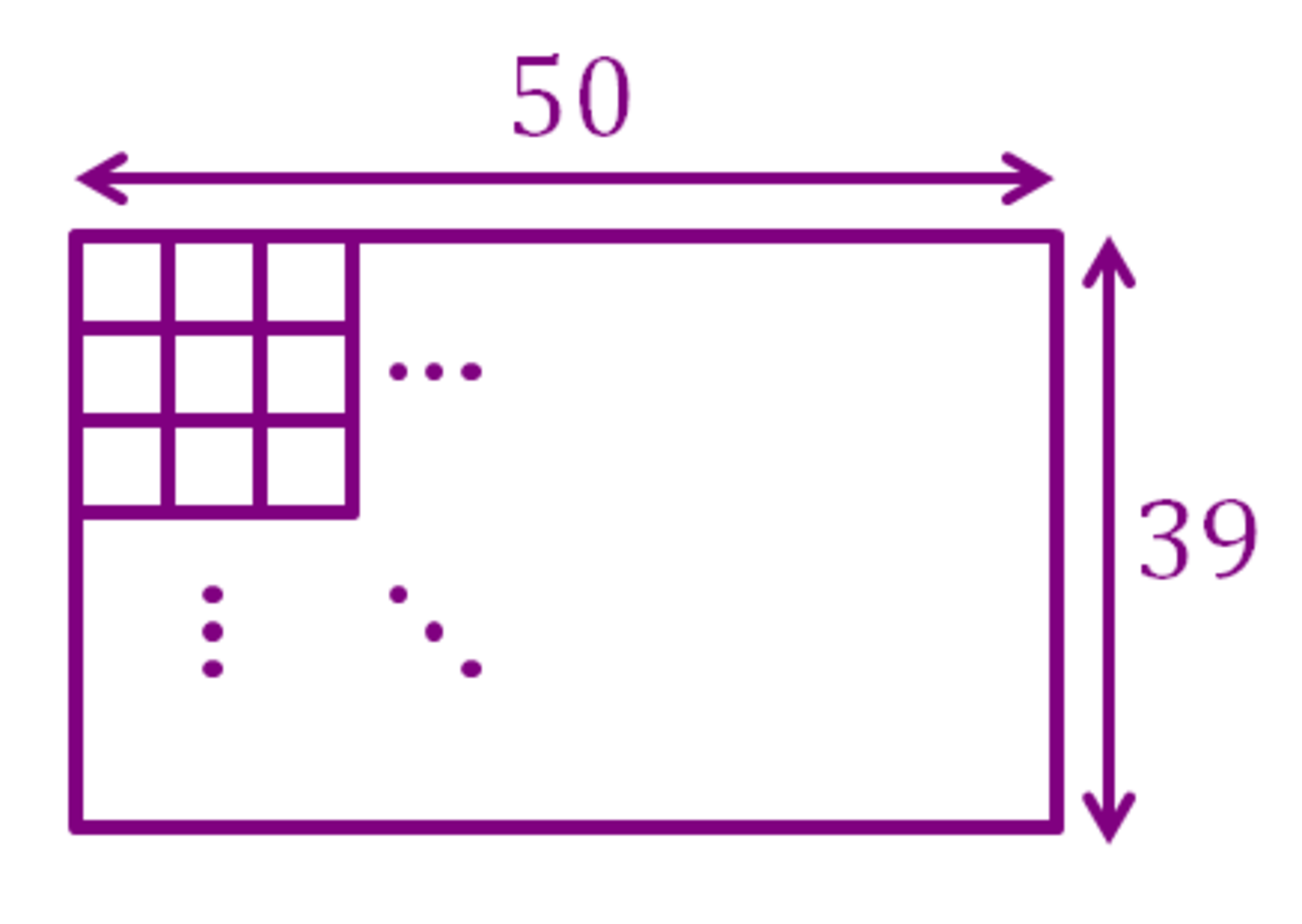
Count the number of 3 × 6 3\times6 rectangles in the 50 × 39 50\times39 grid above.

I'm lazy to draw new grids by the way.

Details and assumptions:

  • Dimensions are expressed as width × \times height . Thus a 3 × 6 3\times6 rectangle (that is, a rectangle of width 3 and height 6) is considered to be different to a 6 × 3 6\times3 (width 6 height 3) rectangle, in this case, you only want the 3 × 6 3\times6 rectangles, not the 6 × 3 6\times3 ones.
This is one part of Quadrilatorics .


The answer is 1632.

Kenneth Tan by Kenneth Tan , 21, Malaysia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Kenneth Tan
Mar 17, 2016

From this note , we know that the number of x × y x\times y rectangles in an a × b a\times b grid given that x ⩽ a x\leqslant a and y ⩽ b y\leqslant b is ( a − x + 1 ) ( b − y + 1 ) (a-x+1)(b-y+1)

Now, substitute a = 50 a=50 , b = 39 b=39 , x = 3 x=3 , y = 6 y=6 into the equation above we would get 1632 1632 .

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Ashish Menon
Mar 25, 2016

In a figure, the number of ( a × b ) (a×b) rectangles in a ( x × y ) (x×y) figure , where x ≥ a x \geq a and y ≥ b y \geq b can be found by the formula :- ( x − ( a − 1 ) ) ( y − ( b − 1 ) ) (x -(a-1))(y-(b-1))
= ( 39 − ( 6 − 1 ) ) ( 50 − ( 3 − 1 ) ) (39 -(6-1))(50-(3-1))
= ( 39 − 5 ) ( 50 − 2 ) (39 -5)(50-2)
= ( 34 × 48 ) (34×48)
= 1632 1632 rectangles. □ _\square



0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...