Count the number of isomorphisms

Probability Level 3

Graph Isomorphism is to check if two graphs that look different are actually the same. More formally, given two graphs does there exist a 1-to-1 mapping of vertices in one graph onto the vertices of other such that edges and non-edges are preserved?. Count the number of isomorphisms of the given graph.

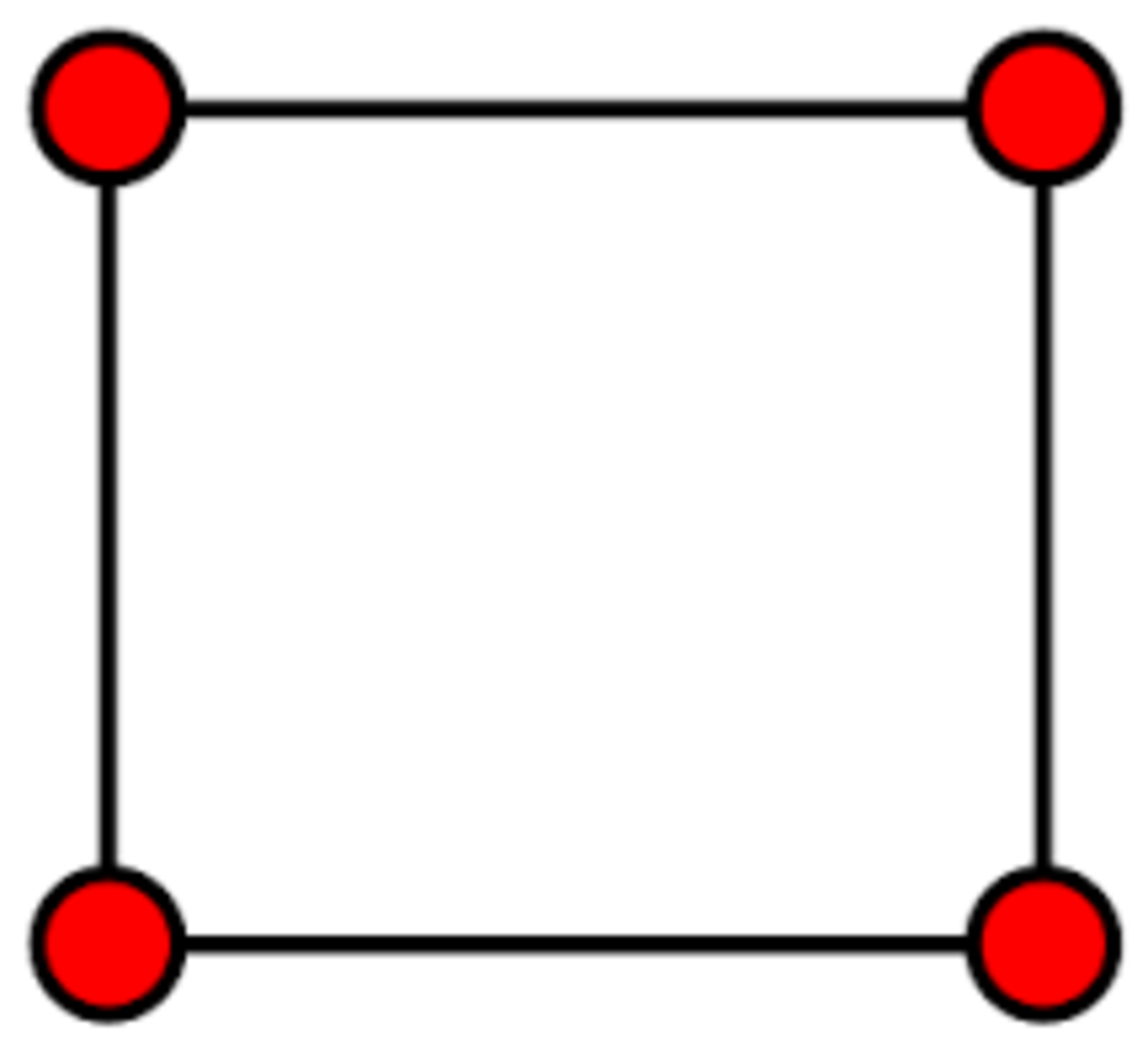
Note : {a,b,c,d} is the vertex set of the given graph.

The answer is 8.

1 solution

Shivdutt Sharma
Dec 9, 2016

There are four vertices in the graph {a,b,c,d}, now a can be map to vertex a or b or c or d once we mapped a then b have 2 choices. So 4 *2 =8

(The question and solution have been edited. This comment is no longer valid.)

Why are there 3 choices for b?
Why does 4 choices and 3 choices lead to $4! = 4 \times 3 \times 2 \times 1$ choices?

I believe the answer should be 8, where there are 2 possibilities for $b$ (and the rest are fixed).

Calvin Lin Staff - 4 years, 6 months ago

Yes it is 8 not 24. i have edited my answer.

shivdutt sharma - 4 years, 6 months ago

Thanks. I have updated the answer to 8.

Calvin Lin Staff - 4 years, 6 months ago

Count the number of isomorphisms

The answer is 8.

1 solution

0 pending reports