Count the Symmetric Binary Trees
A binary tree is symmetric if the right subtree is a mirror image of the left subtree. For example, there are 9 nodes in the following tree.
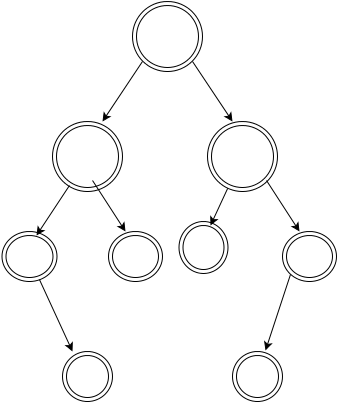
How many symmetric binary trees with 11 nodes are there?
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let C n = n + 1 1 ( n 2 n ) be the n -th Catalan number . We claim that the number of symmetric binary trees of 2 n + 1 nodes is C n .
First, we need one node as the root. Since the tree is symmetric, constructing the left subtree completely decides the right subtree; just mirror the whole thing. If the left subtree has k nodes, then so as the right subtree, so the total number of nodes is 2 k + 1 . Thus we need k = n .
Now, whatever the left subtree is gives exactly one symmetric tree. So all we need to do is to compute the number of binary trees of n nodes; this number is equal to the number of symmetric binary trees of 2 n + 1 nodes. This number is C n , as proved in the wiki article linked above.
The problem asks for n = 5 , thus the answer is C 5 = 6 1 ( 5 1 0 ) = 4 2 .