Counting Boring Squares

Probability Level 4

A 3 × 3 3 \times 3 boring square is (as defined in this problem ) is a 3 × 3 3 \times 3 grid filled with integers 1 , 2 , . . . , 9 1,2,...,9 such that the sum of the integers is unique in every row, column and diagonal.

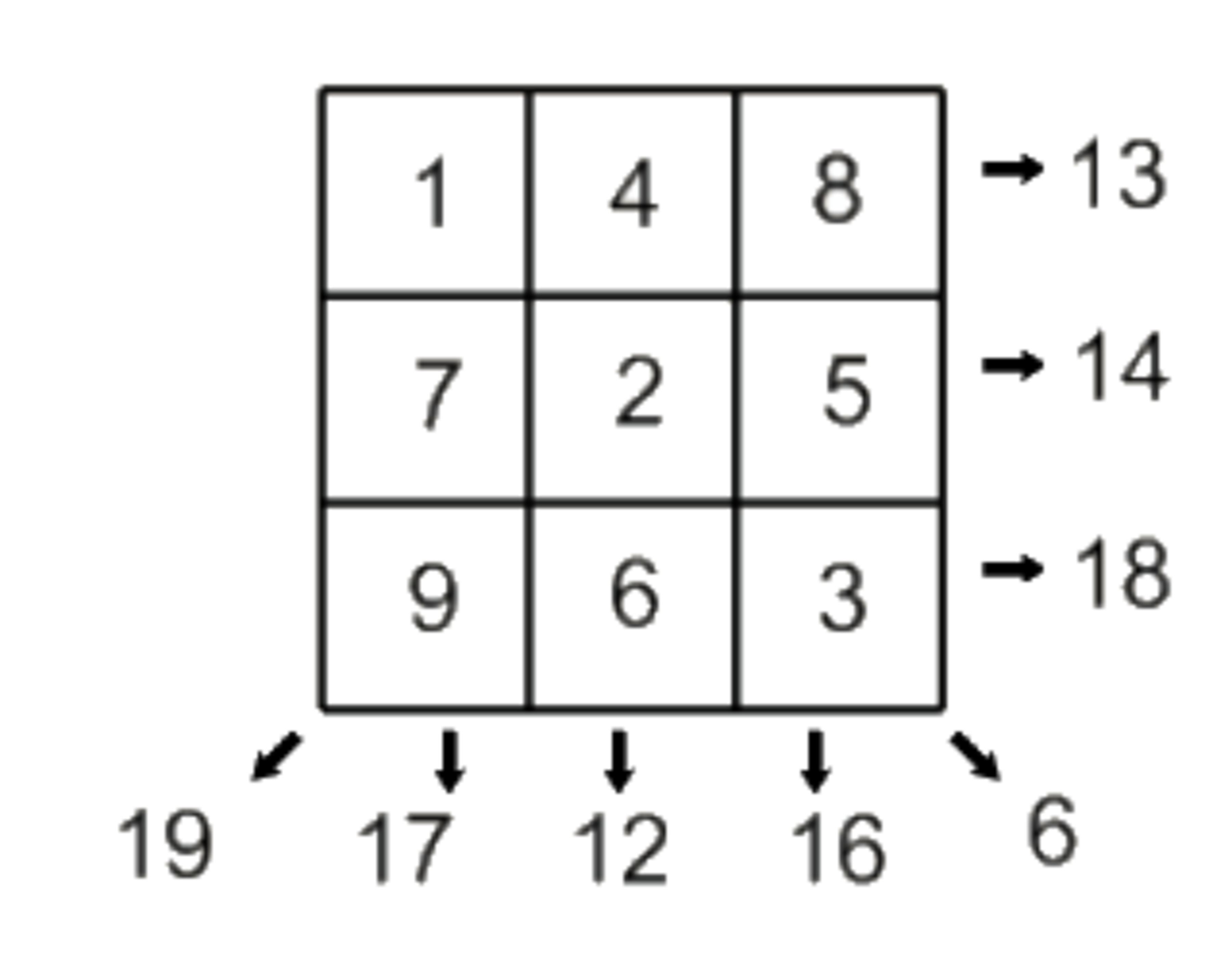
How many 3 × 3 3 \times 3 boring squares are there ?

NB : Squares that are rotations or reflections of each other are considered the same.


The answer is 3120.

Romain Bouchard by Romain Bouchard , 34, France

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Arjen Vreugdenhil
Dec 18, 2017

Brute force method

The following code counts 24960 24960 boring squares. They can be grouped into sets of eight identical squares (under rotation/reflection), so that the answer is 24960 / 8 = 3120 24960/8 = \boxed{3120} . 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
 
sq = [1,2,3,4,5,6,7,8,9]
N = 0

while sq > []:
    while len(sq) < 9:
        i = 1
        while i in sq:
            i = i + 1
        sq.append(i)

    s1 = sq[0] + sq[1] + sq[2]
    s2 = sq[3] + sq[4] + sq[5]
    s3 = sq[6] + sq[7] + sq[8]
    s4 = sq[0] + sq[3] + sq[6]
    s5 = sq[1] + sq[4] + sq[7]
    s6 = sq[2] + sq[5] + sq[8]
    s7 = sq[0] + sq[4] + sq[8]
    s8 = sq[2] + sq[4] + sq[6]

    sums = set([s1,s2,s3,s4,s5,s6,s7,s8])
    if len(sums) == 8:
        N = N+1

    i = 10
    while i > 9 and len(sq) > 0:
        i = sq[-1]
        del sq[-1]
        i = i + 1
        while i <= 9 and (i in sq):
            i = i + 1

    if i <= 9:
        sq.append(i)

print(N)

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...