Counting Money

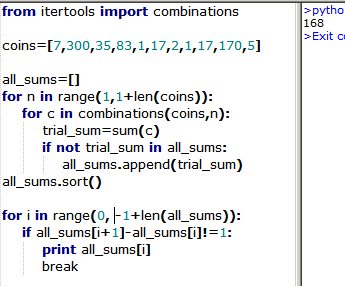
Let us follow the hint. Using just the first two coins, it is possible to pay any amount from 0 to 2. If we include the third coin, 2, the range of amounts that can be paid extends to from 0 to 4. What if we include coin 5? Can we pay any amount of money from 0 to 4+5=9? Yes, for any amount from 0 to 4, we do not have to use coin 5, and for any amount x from 5 to 9, we use coin 5 and the amount x−5 can be paid using the remaining coins.

In general, if the range of amounts that can be paid using the first k coins is from 0 to r, and the following coin has value x, then either:

• $x \le r + 1$ and it is possible to pay any amount from 0 to r + x using the first k + 1 coins, or

• $x>r + 1$ and it is not possible to pay the amount of r + 1, since x and all the following coins have greater values.

Using this observation, we obtain the following sequence of included coins and ranges of amounts that can be paid:

And finally, 170 > 168 + 1 = 169, so the smallest amount that cannot be paid using the given coins is $\boxed{169}$ .

Ultra brute force!

Form all possible sums, then look for the first gap in the sorted list of these sums. Mr Mehta's solution is ever so slightly more subtle. ;)

Using a greedy algorithm in Python.

def change(val,coins):
    if val==0:
        return []
    poss = [x for x in coins if x <= val]
    if poss==[]:
        return []
    a = max(poss)
    coins.remove(a)
    return [a]+change(val-a,coins)
for x in range(1,700):
    if sum(change(x,[1,1,2,5,7,17,17,35,83,170,300])) != x:
        print x
        break

Python 2.7:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

from itertools import product
coins = (1,1,2,5,7,17,17,35,83,170,300)
sums = set()
for exists in product((True, False), repeat=len(coins)):
    new = 0
    for coin in xrange(len(coins)):
        if exists[coin]:
            new += coins[coin]
        sums.add(new)
guess = 1
while guess in sums:
    guess += 1
print "Answer:", guess