Counting Routes!
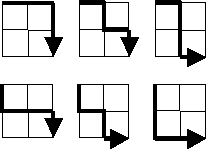
The image shows the ways(routes) through which one can go from one point to the other in a grid.
How many different routes can you find through a grid?
Note :This can be generalized for grid
Also try
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each number on the grid represents the number of routes to that node (intersection point on the grid).
For example, consider the node which has 1 5 routes to it on the bottom row.
As there are 1 0 routes to the node above it and 5 routes to the node on its the right , there are 1 0 + 5 = 1 5 routes to it in total.
In the same way, each of the other values have been calculated and it becomes apparent that the total number of different routes through a 4 × 4 , g r i d , i s , 7 0 .
G e n e r a l i z a t i o n - Observe these using the Pascal's triangle. The number of routes are circled with red color.
Routes for 1 × 1 grid = ( 1 2 ) = 2 .
Routes for 2 × 2 grid = ( 2 4 ) = 6 .
Routes for 3 × 3 grid = ( 3 6 ) = 2 0 .
Routes for 4 × 4 grid = ( 4 8 ) = 7 0 .
…
…
Routes for n × n grid = ( n 2 n ) = n ! × n ! ( 2 n ) ! :)