Counting squares... in rectangles.
For an a × a grid of unit squares, the total number of squares of different sizes is given by:
N a × a = n = 1 ∑ a n 2
For example, for a = 5 , N 5 × 5 = 1 + 4 + 9 + 1 6 + 2 5 = 5 5 . Now rather than looking at a perfect square grid, lets look at rectangular grids.
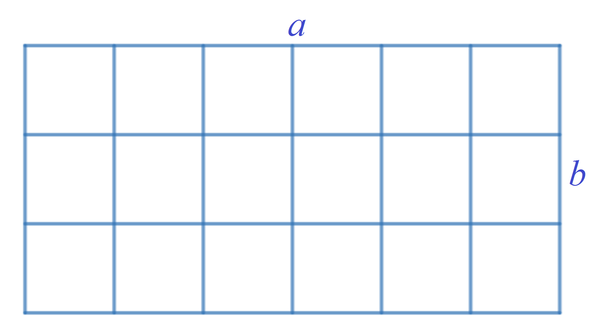
Find N a × b , the total number of squares in a a × b grid, where a > b .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Martin Taylor , the answer should be n = 0 ∑ b − 1 ( a − n ) ( b − n ) . See my solution. In your problem statement 1 + 4 + 9 + 1 6 + 2 5 = 5 5 and not 3 9 . Why use uppercase A and B in diagram and question but lowercase a and b in answer. I have done all the changes for you.
oh thanks for pointing that out, will fix
For an a × b grid, where a > b , we note that the number of 1 × 1 squares in the grid n 1 = a b , the number of 2 × 2 squares in the grid n 2 = ( a − 1 ) ( b − 1 ) , n 3 = ( a − 2 ) ( b − 2 ) , ... n b = ( a − b + 1 ) ( b − b + 1 ) , Therefore
N a × b = n 1 + n 2 + n 3 + ⋯ + n b = a b + ( a − 1 ) ( b − 2 ) + ( a − 2 ) ( b − 2 ) + ⋯ + ( a − b + 1 ) ( b − b + 1 ) = n = 0 ∑ b − 1 ( a − n ) ( b − n )
Lets express the squares as the top left corner, for example for a 3 by 3 square it can be expressed as this.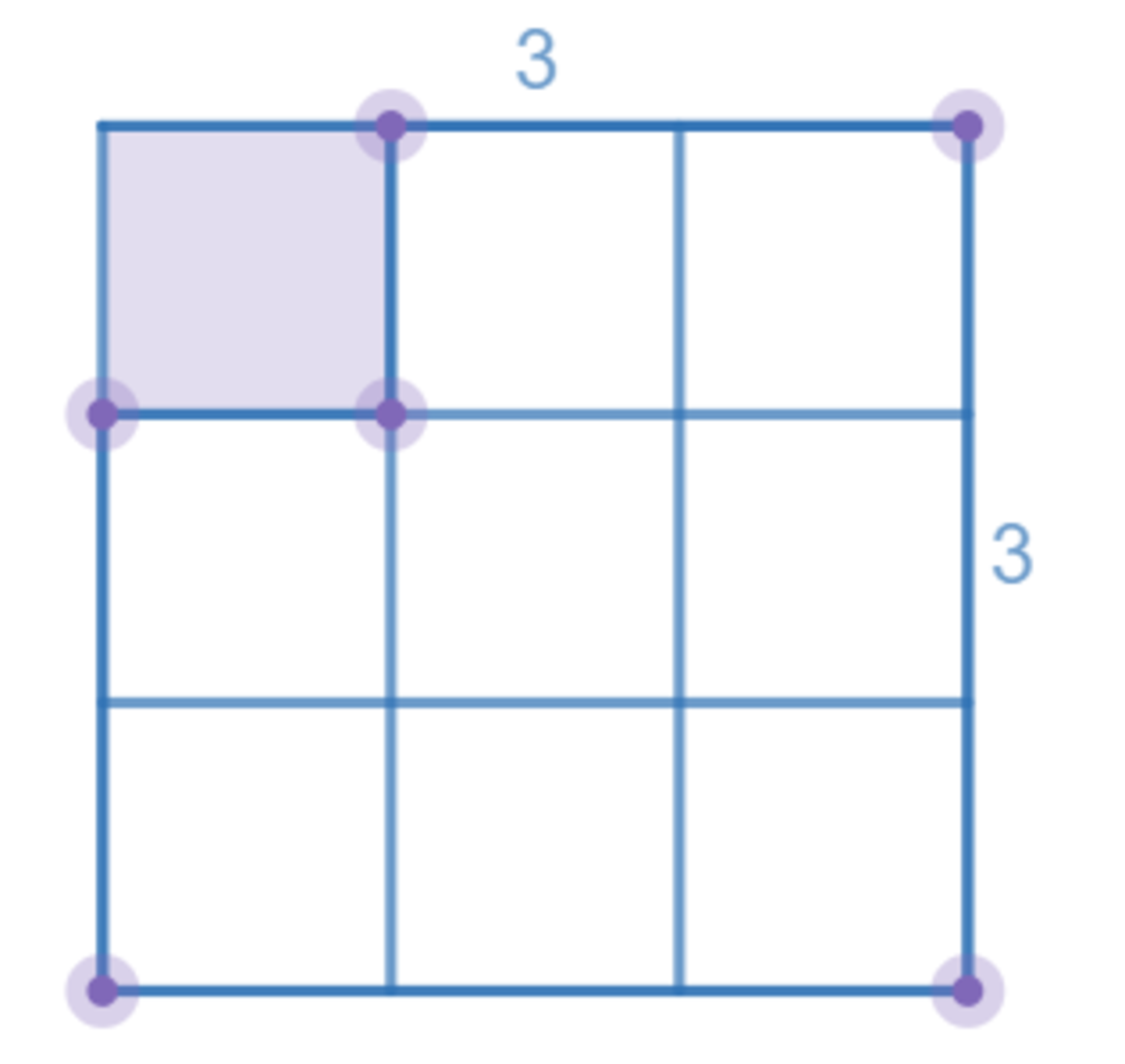 this helps as it simplifies the problem ...
this helps as it simplifies the problem ...
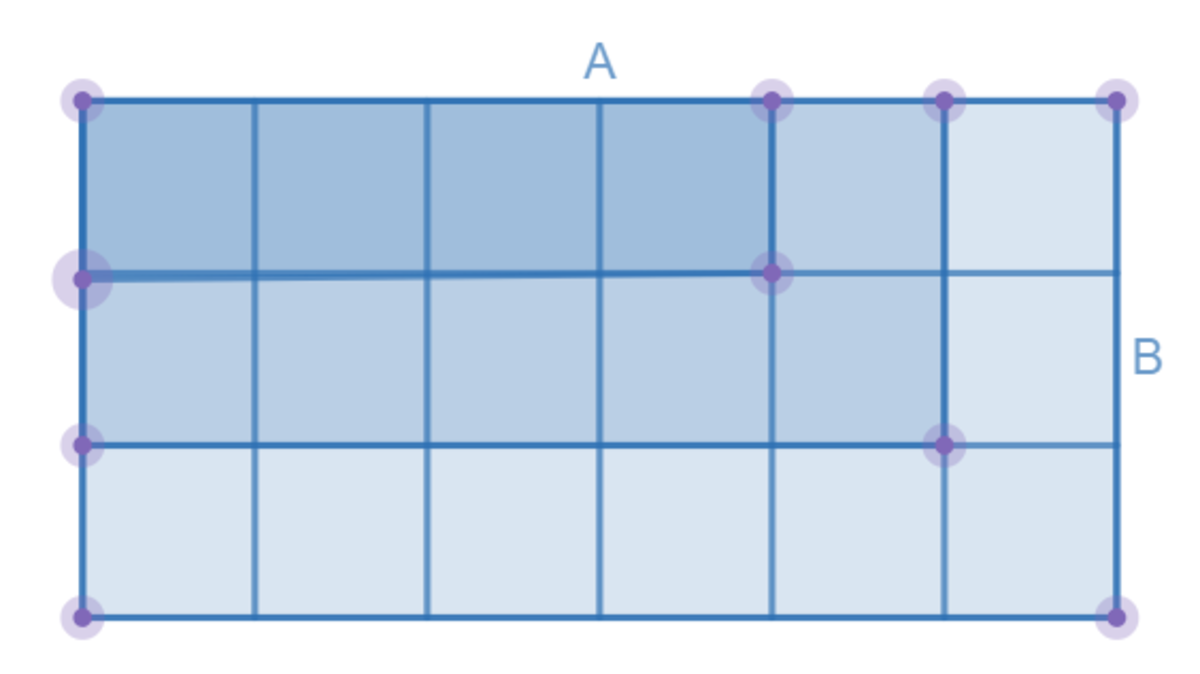 Showing where each square goes turns the problem from a more complex puzzle into a simple geometry question.
Showing where each square goes turns the problem from a more complex puzzle into a simple geometry question.
using this information we can work out that the formula is n = 1 ∑ b − 1 ( a − n ) ( b − n )