Counting the Shaded Squares.
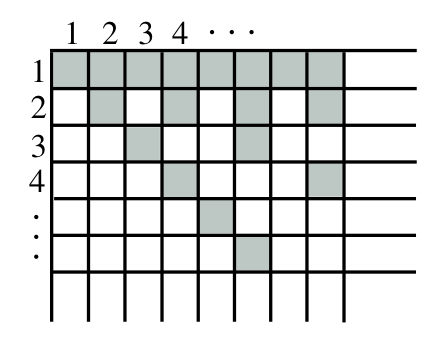 In the diagram, the grid has
rows and
columns, numbered from 1 to
. In row
, every box is shaded. In row
, every second box is shaded. In row
, every third box is shaded. The shading continues in this way, so that every
box in row
is shaded.
In the diagram, the grid has
rows and
columns, numbered from 1 to
. In row
, every box is shaded. In row
, every second box is shaded. In row
, every third box is shaded. The shading continues in this way, so that every
box in row
is shaded.
Among the given answers, which column has the greatest number of shaded boxes?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the row number and column number be r and n respectively. We note that r th row has all n m o d r = 0 boxes shaded. This means that the number of boxes shaded in n th column is the number of divisors of n .
Now let us check the numbers of divisors of the answer options.
Therefore, column 6 0 has the greatest number of shaded boxes.