Counting triangles and lines

Consider 8 vertices of a regular octagon and its center. If denotes the number of triangles and denotes the number of straight lines that can be formed with these 9 points, then the value of is a 2-digit integer . Find the value of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we count the total number of lines i.e. ( 2 8 ) = 2 8 . [ Since there are 8 vertices and taking any two of them will give us an unique line ]
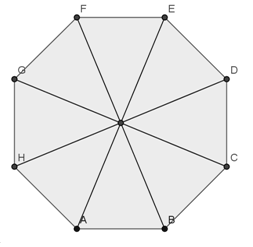
N o t e : Any line from the centre to any vertex is already counted while counting the diagonals. So need of counting it later.
Now we have to count the number of triangles. For that we require 3 points. Thus ( 2 9 ) = 8 4 [8 vertices and the centre]
But we have to subtract 4 cases where the 3 points which are chosen becomes collinear i.e. the diagonals
Namely AOE , BOF , COG , DOH are counted which shouldn't be counted in triangles.
Thus T = 8 4 − 4 = 8 0
S = 2 8
T − S = 8 0 − 2 8 = 5 2
Hence
a + b = 5 + 2 = 7