Coupled Lines

Each line has the form $y - 7 = m(x + 6) \longrightarrow mx - y + 6m + 7 = 0.$ Using the point to line distance formula, we'll use this line and the origin to derive the following equation:

$\frac{\left|m(0) - 1(0) + 6m + 7\right|}{\sqrt{m^2 + 1}} = 2$

Multiply both sides of $\sqrt{m^2 + 1}$ and then square both sides to obtain

$36m^2 + 84m + 49 = 4m^2 + 4 \longrightarrow 32m^2 + 84m + 45 = 0 \longrightarrow (8m + 15)(4m + 3) = 0$

This implies the two slopes are $-\frac{15}{8}$ and $-\frac{3}{4}$ , which sum to -2.625

$Let~~ A(-6,7),~O(0,0),~~AOT_1~ and~ AOT_2, ~be~ the~ two~ rt~ \angle~ \Delta s~ formed,\\ with~rt \angle~ at~ T_1,~and~T_2.\\ AO=\sqrt{(-6)^2+7^2)}=\sqrt{85}.\\ \text{Angle AO makes with x-axes is } =Tan^{-1}\dfrac 7 {-6}=180-49.3987 =130.6013^o.\\ The~ angle~ T_1AO=T_2AO=Sin^{-1}\dfrac 2 {\sqrt{85}}=12.5288^o. 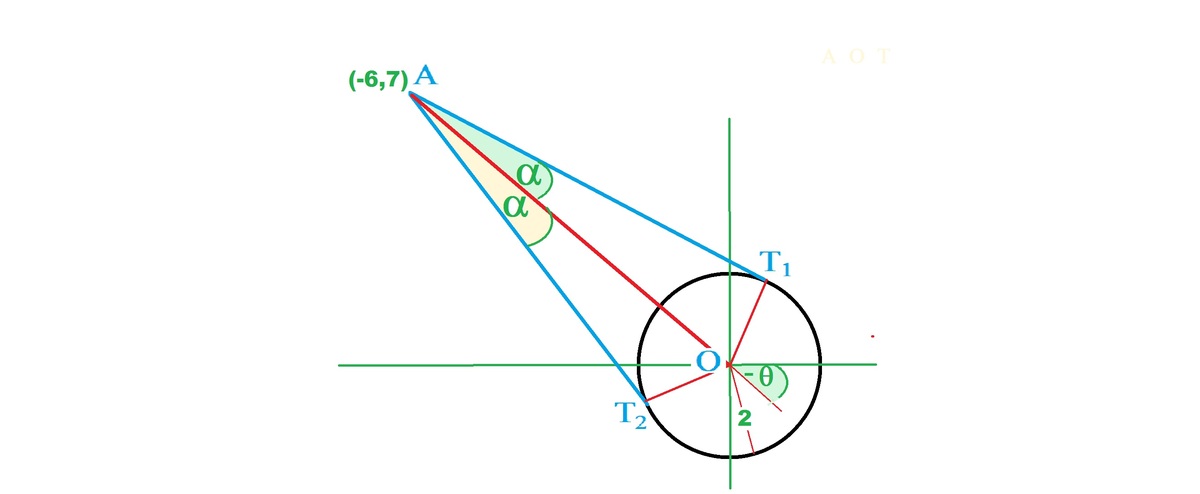\\ So~ tangents, ~AT_1 ~and~ AT_2~ make~angles~\pm~12.5288^o~ with~ AO.\\ So ~the~ sum ~of~ the~ slopes =Tan(130.6013 + 12.5288) + Tan(130.6013 - 12.5288) \\ =\Large ~~~~\color{#D61F06}{- 2.625}$ $OR$ The lines are the two tangents to $x^2+y^2=4$ from( - 6, 7). Let L be segment joining ( - 6,7) to center (0,0).
Let $\theta$ be angle made by L with +x-axis. $~~~~~~\alpha$ the angle made by tangents with L.
$L=\sqrt{( - 6)^2+7^2}=\sqrt{85}. ~~~~~~~~~~~~Tan\theta=\dfrac{ - 6} 7.~~~~~~~~~ Sin\alpha=\dfrac 2 {\sqrt{85}} , ~~~~~~~~\therefore~Tan\alpha=\dfrac 2 9.\\ \text{The angles made by the lines with +x-axis are }~~~ (\theta+ \alpha)~~~and~~ ~ (\theta- \alpha).\\ Sum ~ of ~ the ~ slope=Tan(\theta+ \alpha)~+Tan(\theta- \alpha)\! =\left(\dfrac{ \frac 7 {- 6}\! +\! \frac 2 9 }{1+\frac 7 {27} } \right)\! +\! \left(\dfrac{ \frac 7 {- 6} - \frac 2 9 }{1-\frac 7 {27} } \right)=\! - \!\dfrac {21} 8= - 2.625$

Another method will be to assume the line as $x\cos { \alpha } +y\sin { \alpha } =2$ and then put in it $(-6,7)$ , thereby giving a trigonometric equation.