Cover a table

Geometry Level 5

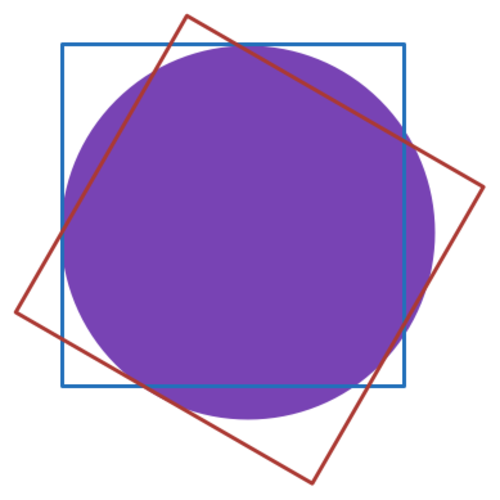A round table is to be completely covered with two unit square tablecloths. Find the maximum value of the diameter of the table.

The answer is 1.172.

1 solution

Joel Toms
Aug 10, 2015

I don't really know how to show there are no better solutions, but this at least would represent a good lower bound.

The black circle represents the table (radius $r$ ) and the blue and red squares represent the tablecloths. Measurements are taken from the blue square.

Using notation on the diagram, the arithmetic is fairly simple. All angles are in degrees.

$\frac pr=\sin(45)=\frac1{\sqrt2}$

$\Rightarrow p=\frac r{\sqrt{2}}.$

$r+p=1$

$\Rightarrow r+\frac r{\sqrt{2}}=1$

$\Rightarrow r\left(1+\frac1{\sqrt2}\right)=1$

$\Rightarrow r\left(\frac{2+\sqrt2}2\right)=1$

$\Rightarrow r=\frac2{2+\sqrt2}$

$\Rightarrow\textrm{diameter of table}=\frac4{2+\sqrt2}=\boxed{1.17157\dots}$

Well I found it interesting to note that diameter of this circle is twice the diameter of the largest circle, two of which would fit in a unit square. Can the answer be worked back from there?

Vishnu Bhagyanath - 5 years, 10 months ago

That is interesting, because it is much easier to say that this solution is optimal. If we say that the square has side 2, then of course our circle is the same size as in this question. I can't pin it together unfortunately so let's wait for someone else's brain to come along.

Joel Toms - 5 years, 10 months ago

Cover a table

The answer is 1.172.

1 solution

0 pending reports