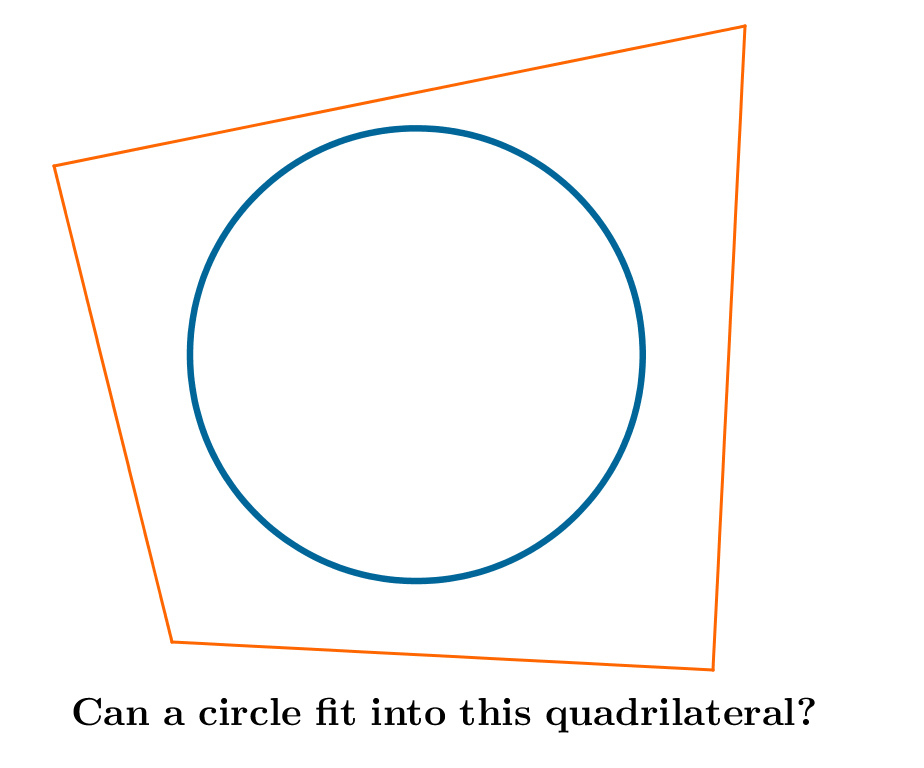
Cover it!

Lets write a rectangle for each side (inward), with sides $\dfrac{A}{P}$ and the sides of the quadrilateral. If the sides of the quadrilateral are $a, b, c, d,$ then the sum of the areas of the rectangles: $a\dfrac{A}{P}+b\dfrac{A}{P}+c\dfrac{A}{P}+d\dfrac{A}{P}=(a+b+c+d)\dfrac{A}{P}=A$ Since, each angle is less than 180 degrees, the quadrilateral will have parts which are part of minimum two rectangles. From that there will be points inside the quadrilateral, which are not covered. These points may be the center of the circle.

The diagonal of the quadrilateral divides it into 2 triangles. The radius $r$ of the incircle of the bigger triangle is equal to $2*A_t / P_t$ where $A_t$ is the area of the triangle and $P_t$ is its perimeter

$r=2*A_t /P_t \geq A/ P$ because $2*A_t \geq A$ and $P_t < P$