Cover Me

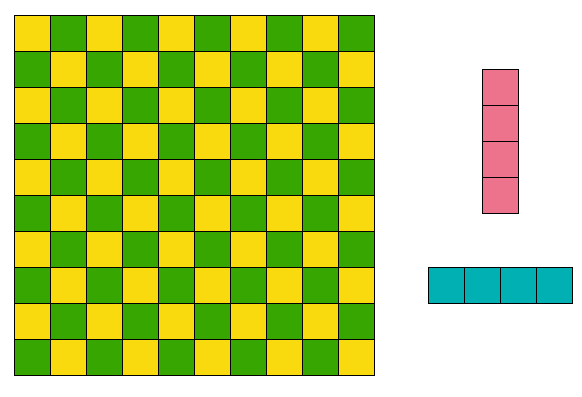
I will prove that an $n \times n$ grid of squares can only only be tiled by $1 \times 4$ tiles completely if $4 \mid n$ . Note that $n$ must be even (or else, there are an odd number of squares which must be tiled 4 at a time, which is impossible).

If $4 \mid n$ , we can tile easily by just tiling as so (example is for $n=8$ :

If $2 \mid n$ , but $4\nmid n$ , then $\frac{n}{2}$ is odd. If we consider the following colouring, it will become apparent soon why this can't be tiled by $1 \times 4$ tiles.

We have coloured $2 \times 2$ blocks of squares. Thus, there are $\frac {n}{2}$ blocks on each side. Notice that this implies there are $\frac {n^2}{4}$ blocks altogether, which is odd, since $\frac{n}{2}$ is odd. Therefore, one colour will have 4 more squares than the other. However, notice that each $1 \times 4$ tile goes through 2 black and 2 white squares. Therefore, this cannot be tiled!

Thus, we have proven that $n \times n$ grids can only be tiled by $1 \times 4$ tiles if $4 \mid n$ .