Cover the chess board
We want to cover an chess board with one square, and with
A) 15 I tetrominoes
B) 15 T tetrominoes
C) 15 L tetrominoes
D) 15 Z tetrominoes
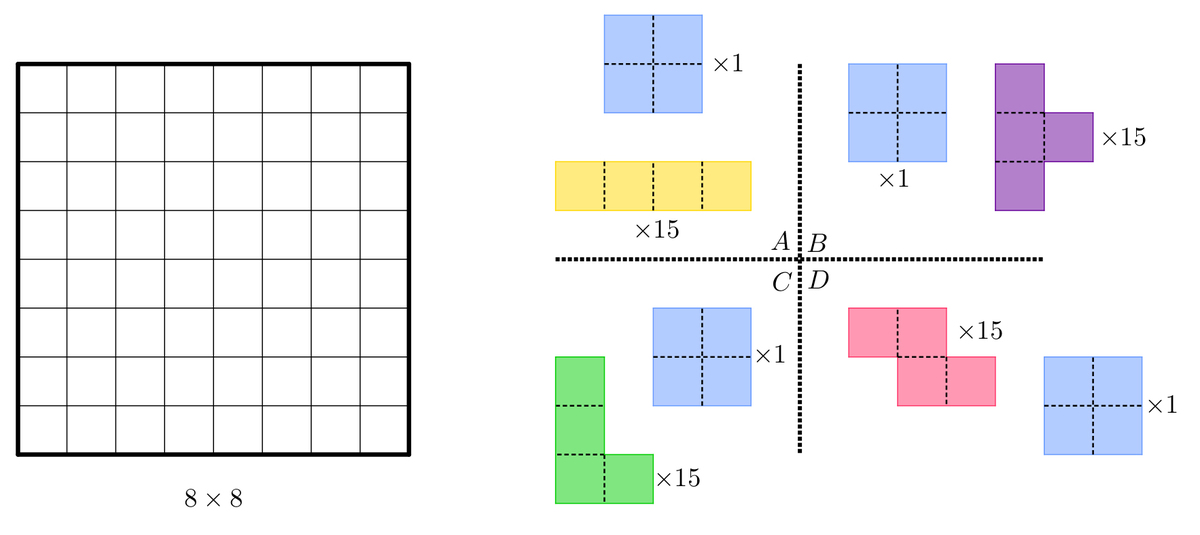
In which case(s) is the covering possible?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A) A 2 × 2 square must cover exactly one black square. Each I tetromino must cover an even number of black squares. Together there are an even number of black squares, but the sum of an odd number and 15 even numbers is an odd number. This is a contradiction.
B) A 2 × 2 square must cover exactly two black squares. Each T tetromino must cover an odd number of yellow squares. Together there are an even number of yellow squares, but the sum of an even number and 15 odd numbers is an odd number. This is a contradiction.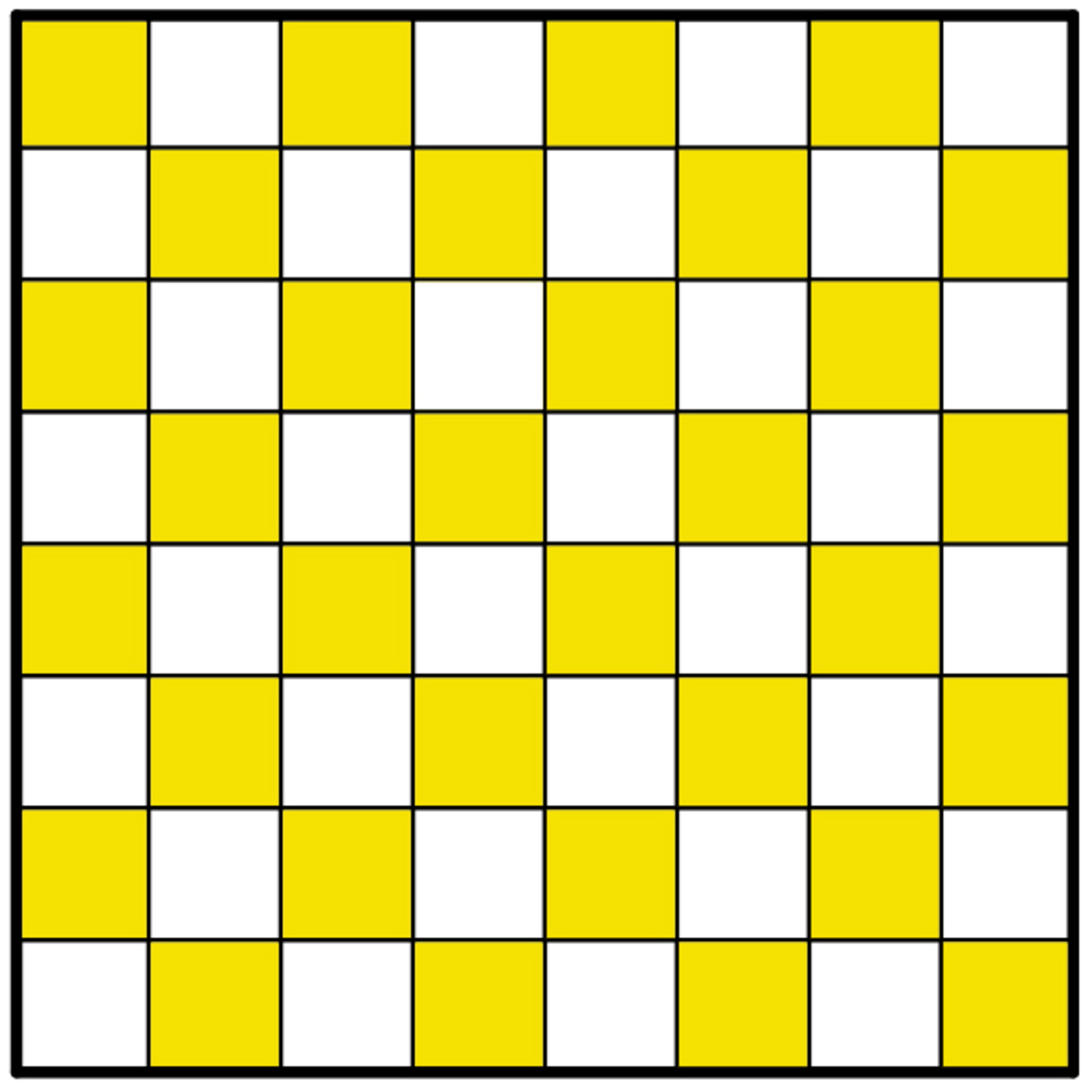
C) A 2 × 2 square must cover exactly two red squares. Each L tetromino must cover an odd number of red squares. Together there are an even number of red squares, but the sum of an even number and 15 odd numbers is an odd number. This is a contradiction.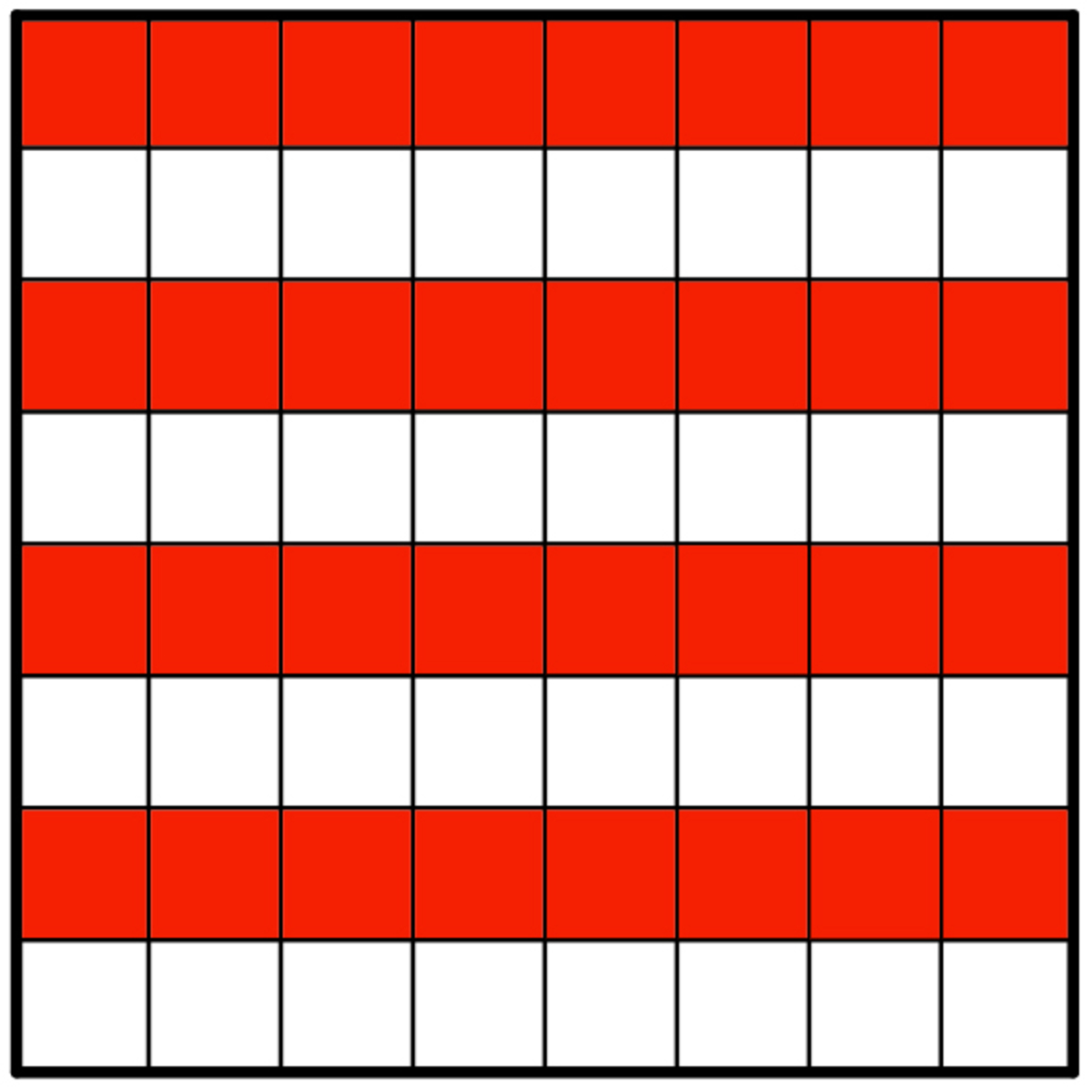
D) A 2 × 2 square must cover an odd number of blue squares. Each Z tetromino must cover an even number of blue squares. Together there are an even number of blue squares, but the sum of an odd number and 15 even numbers is an odd number. This is a contradiction.