Covering a chess board
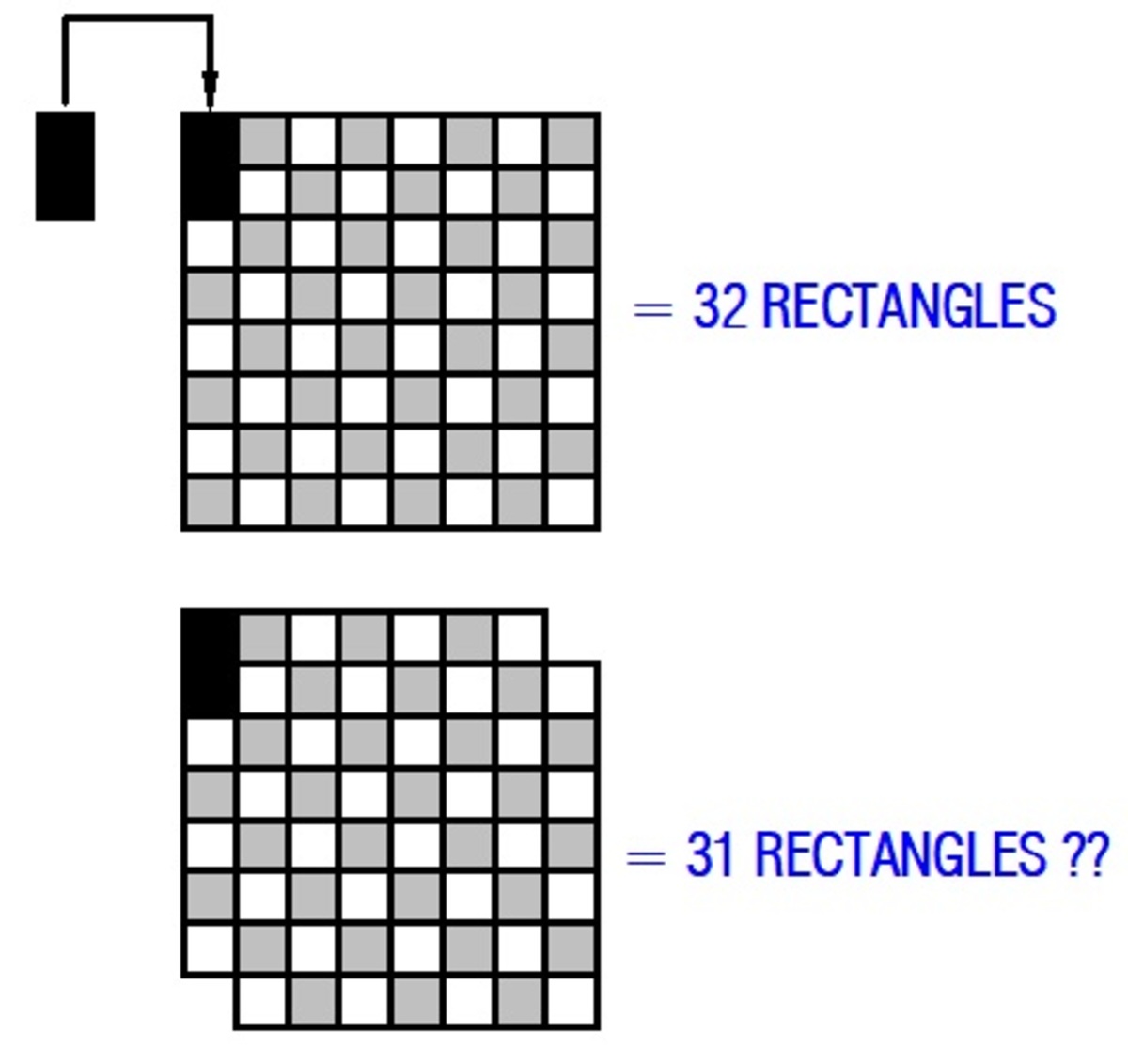A chess board has
squares. This can be completely covered by
cardboard rectangles, each cardboard covering just
squares. Supposing we remove
squares of the chess board at diagonally opposite corners, can we cover the modified board with
cardboard rectangles?
Note: The cardboard rectangle can be rotated in any angle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Look the the second figure (Please replace the black squares by completing the sequence.): There are 32 white squares and 30 black squares. Each rectangle covers 1 white square and 1 black square, so the covering would not be completed.