Covering three spheres with a cone
Three spheres of radius are placed on a table tangent to each other, i.e. with their centers forming an equilateral triangle whose plane is horizontal and parallel to the flat surface of the table. You want to cover the three spheres with a right circular cone whose axis is perpendicular to the surface of the table, and whose semi-vertical angle (the angle between its axis and its curved surface) is , such that the cone is tangent to each of the spheres. How high above the table is the apex of this conical cover ?
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
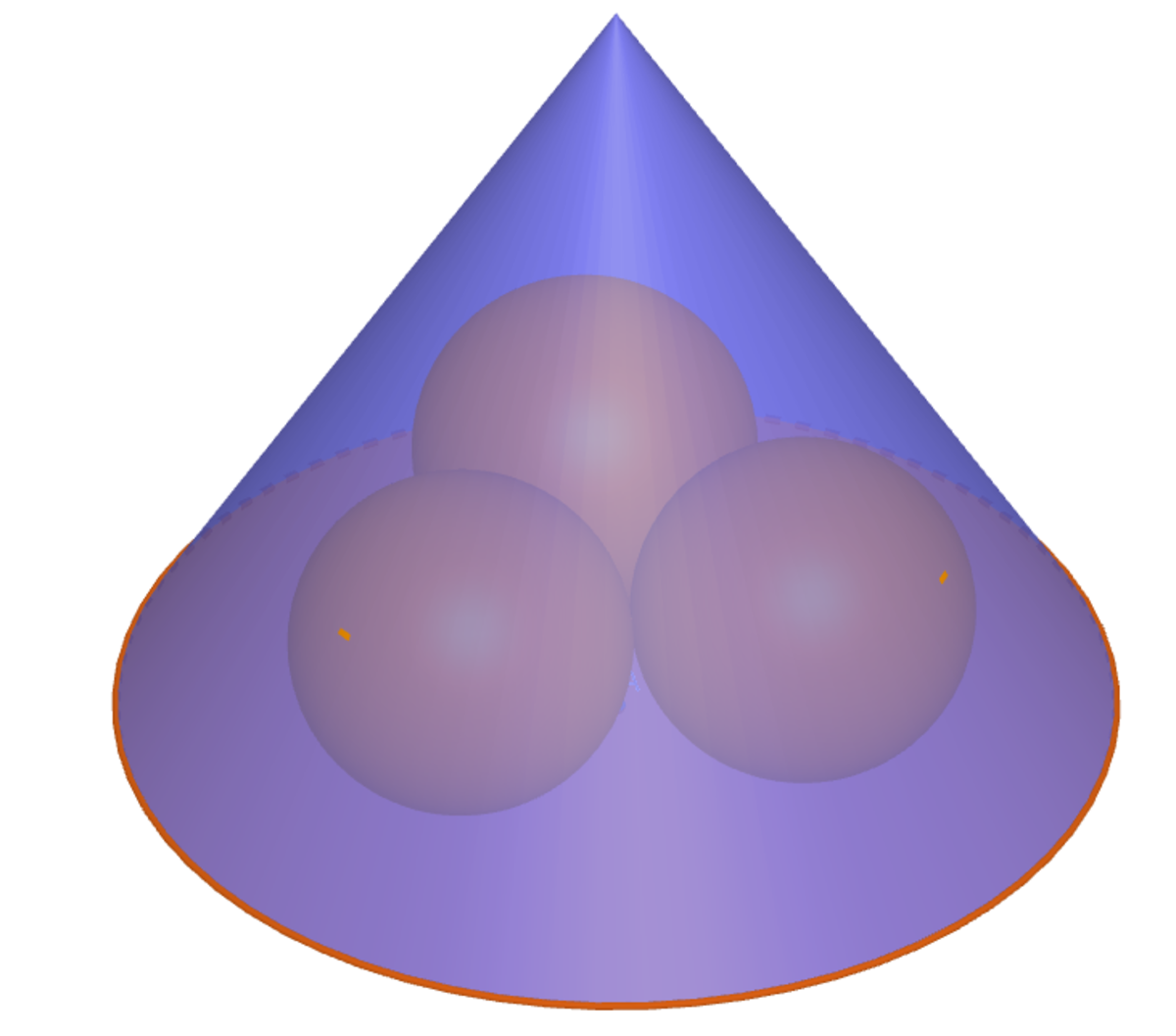
The points where the spheres touch the cone's base make up the vertices of an equilateral triangle with sides 10 + 10 = 20 units. Therefore, the distance between a sphere's center and the cone's axis is equal to the distance between a vertex and the incenter = circumcenter of that equilateral triangle.
With the semi-vertical angle of 30°, the curved surface of the cone would have make a 90° - 30° = 60° angle with the base and this would be bisected into 60° ÷ 2 = 30° by the hypothenuse of a right triangle with its height being the sphere's radius and its length a part of the cone's radius.
By the information collected above, the cone's radius equal the sum of the equilateral triangle's circumradial length plus the right triangle's base length. This is equal to (20 / 2) × (2 / √3) + 10 × √3 = 20/√3 + 10√3 = 50/√3 units.
The height of the cone is just √3 time the cone's radius, so our answer is √3 × (50/√3) = 50 units.