Cow pasture
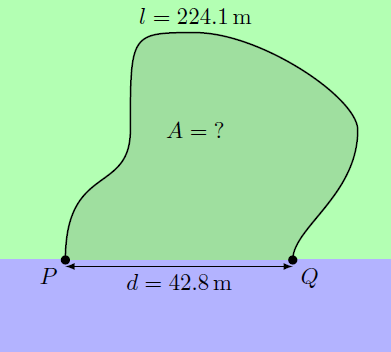
A farmer wants to fence a cow pasture on a riverbank. He has a wire fence with a total length of available. The beginning and end point of the fence (points and ) are fixed in advance and have a distance from each other. The farmer can choose an arbitrary shape for the cow pasture. What is the maximum possible area of the pasture? Give the answer in square meters and round it to the next integer.
The answer is 5589.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This problem is special case for an isoperimetric problem. The shape, that maximizes the area for a given perimeter, is a circle. Therefore, we can sketch the solution as follows: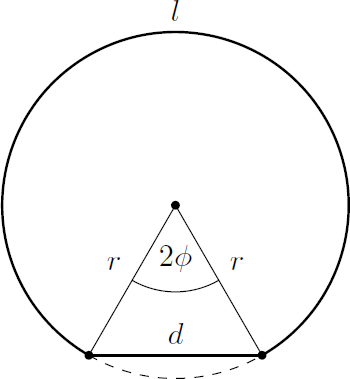 For a circle with radius
r
and a triangular segement with angle
2
ϕ
we can rewrite the quantities
d
and
l
by
d
l
⇒
l
d
=
2
r
sin
ϕ
=
2
(
π
−
ϕ
)
r
=
π
−
ϕ
sin
ϕ
≈
0
.
1
9
0
9
9
The numerical solution for
ϕ
results
ϕ
≈
0
.
5
2
3
6
0
9
≈
3
0
∘
Therefore,
r
≈
d
and
A
=
(
π
−
ϕ
+
sin
ϕ
cos
ϕ
)
r
2
≈
(
6
5
π
+
4
3
)
r
2
≈
5
5
8
9
m
2
For a circle with radius
r
and a triangular segement with angle
2
ϕ
we can rewrite the quantities
d
and
l
by
d
l
⇒
l
d
=
2
r
sin
ϕ
=
2
(
π
−
ϕ
)
r
=
π
−
ϕ
sin
ϕ
≈
0
.
1
9
0
9
9
The numerical solution for
ϕ
results
ϕ
≈
0
.
5
2
3
6
0
9
≈
3
0
∘
Therefore,
r
≈
d
and
A
=
(
π
−
ϕ
+
sin
ϕ
cos
ϕ
)
r
2
≈
(
6
5
π
+
4
3
)
r
2
≈
5
5
8
9
m
2