Cowculus
A cow is tied to a circular barn of radius 6 by a rope just long enough to reach halfway around the circle.
If the area of the region the cow can graze can be expressed as A π 3 , what is A ?
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Albert Lau
Sir, check this
https://brilliant.org/problems/moo/?ref_id=1510821
Here's my approach in brief:
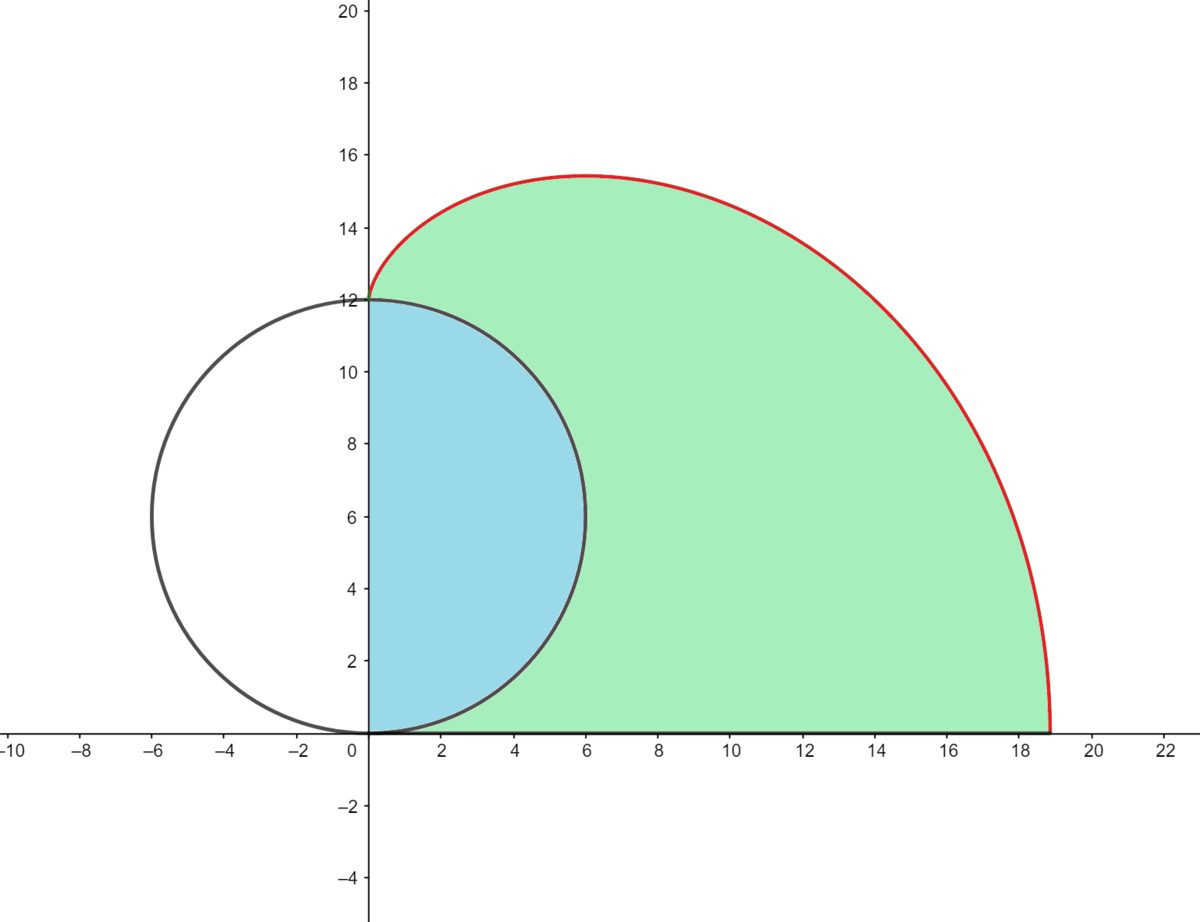 Image made in GeoGebra graphing calculator
Image made in GeoGebra graphing calculator
-
find parametric equation of the red curve: x ( t ) y ( t ) = R ( sin t + ( π − t ) cos t ) = R ( 1 − cos t + ( π − t ) sin t )
-
calculate the green area as: Area = ∫ π 0 y ( t ) ⋅ x ′ ( t ) d t − 2 R 2 π = 6 R 2 π 3 I used WolframAlpha to evaluate this definite integral.
-
calculate the whole area as: 2 × Area + 2 ( R π ) 2 π = 6 5 R 2 π 3 . From here, we deduce that A = 3 0 .

the area can be divided into 3 parts.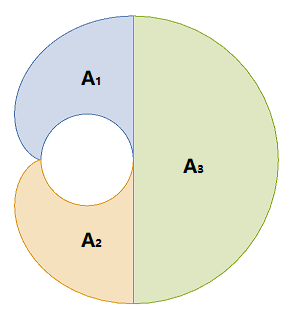 let the radius of the circular barn be r unit, the length of rope will be
π
r
unit.
let the radius of the circular barn be r unit, the length of rope will be
π
r
unit.
A 3 = 2 1 π ( π r ) 2 = 2 1 π 3 r 2 .
for A 1 and A 2 ,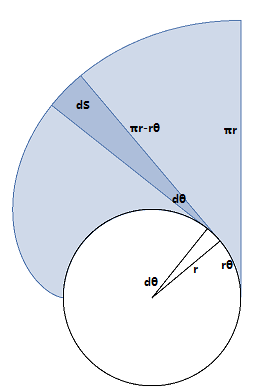 d
S
∫
0
A
1
d
S
A
1
A
2
∴
area
subs
r
=
6
,
area
∴
A
=
2
1
(
π
r
−
r
θ
)
2
d
θ
=
2
1
r
2
(
π
−
θ
)
2
d
θ
=
2
1
r
2
∫
0
π
(
π
−
θ
)
2
d
θ
=
6
1
π
3
r
2
=
A
1
=
6
1
π
3
r
2
=
2
1
π
3
r
2
+
6
1
π
3
r
2
+
6
1
π
3
r
2
=
6
5
π
3
r
2
=
3
0
π
3
=
3
0
d
S
∫
0
A
1
d
S
A
1
A
2
∴
area
subs
r
=
6
,
area
∴
A
=
2
1
(
π
r
−
r
θ
)
2
d
θ
=
2
1
r
2
(
π
−
θ
)
2
d
θ
=
2
1
r
2
∫
0
π
(
π
−
θ
)
2
d
θ
=
6
1
π
3
r
2
=
A
1
=
6
1
π
3
r
2
=
2
1
π
3
r
2
+
6
1
π
3
r
2
+
6
1
π
3
r
2
=
6
5
π
3
r
2
=
3
0
π
3
=
3
0