Crank Generator Power

Electricity and Magnetism Level 4

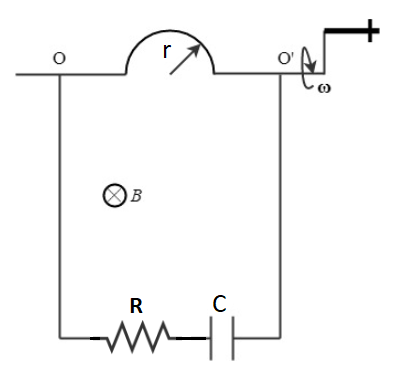
A conducting rod is bent in the shape of a semicircle of radius $r$ and the straight parts along the ends of the diameter of the semicircle are passed through fixed, smooth conducting rings $O$ and $O'.$ A capacitor with capacitance $C$ is connected to the rings with the help of ideal wires. A resistance $R$ is in series with the capacitor. The system is placed in a uniform magnetic field of strength $B$ such that the axis of rotation $OO'$ is perpendicular to the direction of the magnetic field.

The semicircle is now rotated about the axis $OO'$ with a constant angular velocity of $\omega$ . Neglect any self-inductance in the circuit.

What is the average mechanical input power (in Watts) required to keep the semicircle rotating?

Inspiration

Details and Assumptions:

Assume AC steady-state operation
$r = 1 \, \text{m}$
$\omega = 120 \, \pi \,\, \text{rad/s}$
$B = 0.1 \, \text{T}$
$R = 1.0 \, \Omega$
$C = \large{\frac{1}{60 \pi}} \, \text{F}$

The answer is 1402.69.

1 solution

Steven Chase
Sep 18, 2018

From the solution to the previous problem, the induced voltage is:

$\large{V(t) = - \frac{\pi \omega B R^2}{2} sin(\omega t)}$

The RMS voltage is:

$\large{V_{rms} = \frac{\pi \omega B R^2}{2 \sqrt{2}}}$

The capacitive reactance is:

$\large{X_C = \frac{1}{\omega C} = \frac{1}{2}}$

The impedance magnitude is:

$\large{Z = \sqrt{R^2 + X_C^2}}$

Current magnitude:

$\large{I_{rms} = \frac{V_{rms}}{Z}}$

The capacitor contributes nothing to the average power. Only the resistive term matters. $\large{P_{av} = I_{rms}^2 R = 1402.69}$

Crank Generator Power

The answer is 1402.69.

1 solution

0 pending reports