Crayon Coloring Curve

This describes one-quarter of the area inside an astroid , hence the area is $\dfrac{1}{4} \times \dfrac{3}{8} \pi \times 8^{2} \approx \boxed{18.85}$ .

This is just a copy of my solution to this problem, with some small modifications

Placing the paper in the cartesian plane, with the bottom left corner ar (0,0), at any given time, the crayon makes an angle $\theta$ with the horizontal, that goes from $\frac{\pi}{2}$ to $0$ , If you consider a new crayon at angle $\theta'=\theta+h$ , the two crayons intersect at a point $P'$ . As $h\rightarrow 0$ , $P'\rightarrow P$ , and $P$ depends on $\theta$ . All these limit intersection points are points in the edge of the area swept by the sqeegee, and vice-versa. This is the main statement on which this solution is based. *For simplicity, I considered a sqeegee of length $1$ , we'll just have to remember to multiply the area by $8^2$ in the end to get the correct answer. 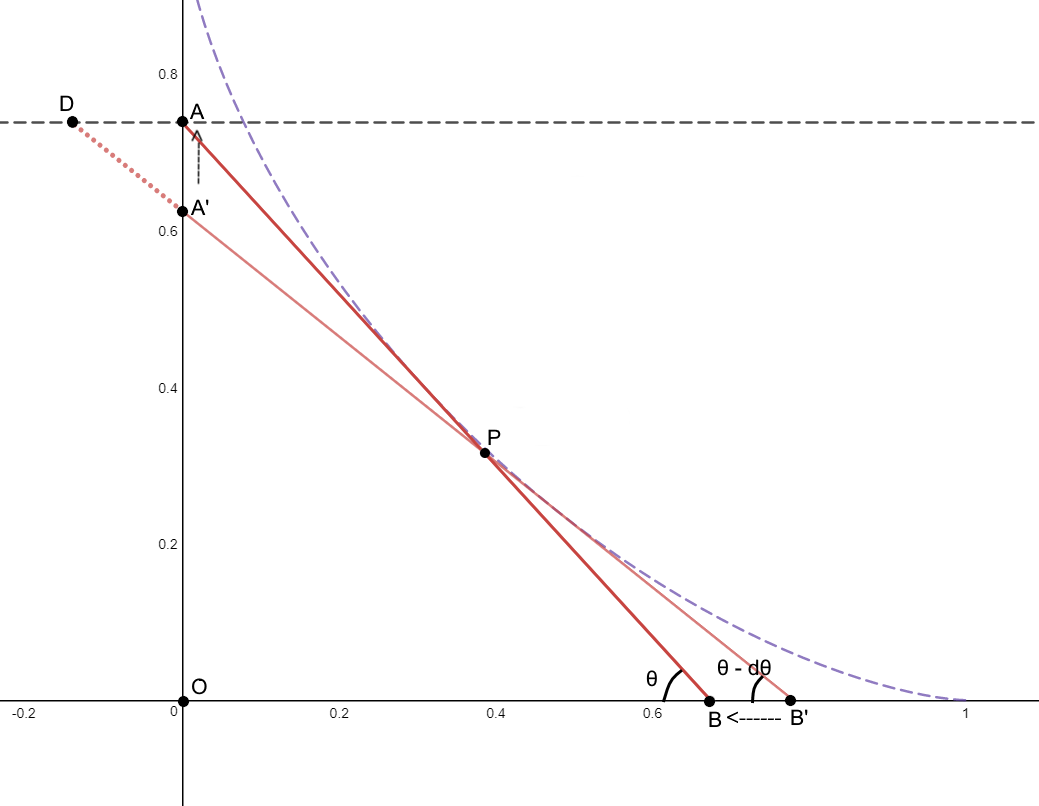Since the crayon has length $1$ , from triangle $\triangle OAB$ , we see that $\overline { AO }=\sin { \theta }$ , $\overline { BO }=\cos { \theta }$ , and consequently, $\overline { AA' } =\cos { \theta } d\theta$ , and $\overline { BB' } =\sin { \theta } d\theta$ . Now, from triangles $\triangle DAA'$ and $\triangle OA'B'$ , we see that $\angle A\widehat { D } A'=\angle A'\widehat { B' } O$ , so $\overline { DA } =\overline { A'A } \cot { \theta }$ which means $\large \overline { DA } =\frac { \cos ^{ 2 }{ \theta } }{ \sin { \theta } } d\theta$ . Finally, from similar triangles $\triangle DAP$ and $\triangle PBB'$ , $\large \frac { \overline { DA } }{ \overline { AP } } =\frac { \overline { BB' } }{ \overline { PB' } }$ , but we know that $\overline { AP } +\overline { PB } =1$ . Then, making $\overline { PB } =p$ and substituting what we found earlier, we have $\frac{\cos^2\theta}{\left(p-1\right)\sin\theta}=\frac{\sin\theta}{p}$ $p=\left(1-p\right)\tan^2\theta$ $p=\frac{\tan^2\theta}{\left(1+\tan^2\theta\right)}$ $p=\sin^2\theta$ Then, the coordinates of the point $P$ with respect to $\theta$ are $x\left(\theta\right)=\cos\theta-\left(\cos\theta\right)\sin^2\theta$ $y\left(\theta\right)=\left(\sin\theta\right)\sin^2\theta$ Simplifying, we have $x\left(\theta\right)=\cos^3\theta$ $y\left(\theta\right)=\sin^3\theta$ Finally, we know that the area under a parametric curve is $\large \int_{t_1}^{t_2}y\left(t\right)x'\left(t\right)dt$ , so substituting for what we have, and multiplying by $8^2$ : $\large Area=64\int_0^{\frac{\pi}{2}}3\sin^4\left(t\right)\cos^2\left(t\right)dt \approx 18.849$

The following web article gives details of an Astroid. We need 1/4 the area $3/8\pi r^2$ , our r=8.
$Area= \frac 1 4*\frac 3 8*\pi* r^2=\frac 1 4*\frac 3 8*\pi* 8^2 = \Huge \color{#D61F06}{18.84955592}.$
link text

A lot of solutions are given here .........