Crazy circles
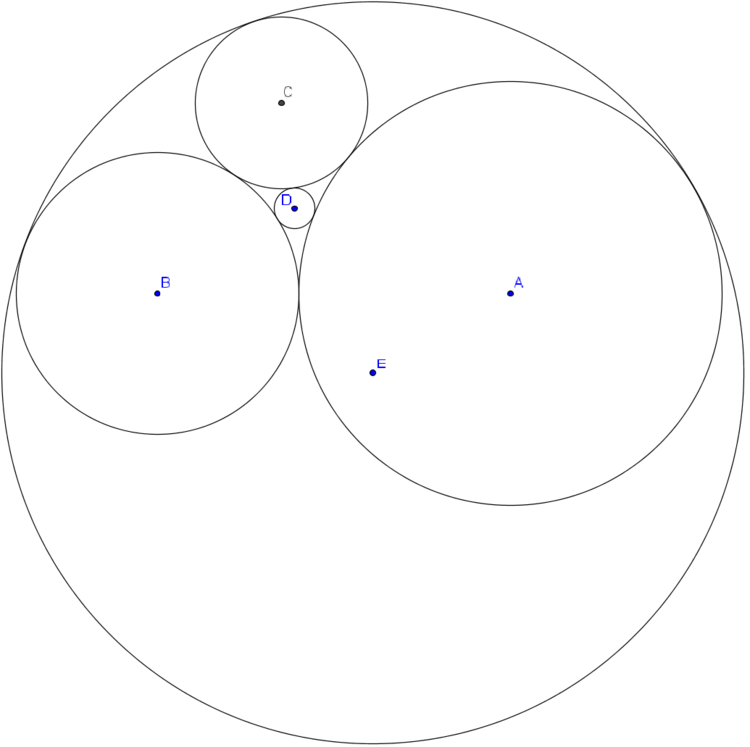 Three circles mutually tangent with centers
A
,
B
and
C
have radii of
2
1
,
1
4
and
c
respectively. Let the circle with center
D
and radius
2
be externally tangent to the three circles, and let the circle with center
E
and radius
R
be internally tangent to the three circles. Find
⌊
1
0
0
(
c
+
R
)
⌋
.
Three circles mutually tangent with centers
A
,
B
and
C
have radii of
2
1
,
1
4
and
c
respectively. Let the circle with center
D
and radius
2
be externally tangent to the three circles, and let the circle with center
E
and radius
R
be internally tangent to the three circles. Find
⌊
1
0
0
(
c
+
R
)
⌋
.
The answer is 4527.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
For two circles of centers ( x 1 , y 1 ) and ( x 2 , y 2 ) and radii r 1 and \(r_2 ) to be tangent to each other, the following equation must be satisfied.
\((x_1-x_2)^2 + (y_1-y_2)^2 = (r_1 \pm r_2)^2\).
Let A ( 3 5 , 0 ) , B ( 0 , 0 ) , C ( x c , y c ) , D ( x d , y d ) and E ( x e , y e ) . The following equations apply.
{ ( x d − 0 ) 2 + ( y d − 0 ) 2 = ( 2 + 1 4 ) 2 ( x d − 3 5 ) 2 + ( y d − 0 ) 2 = ( 2 + 2 1 ) 2
Solving it, we get x d = 1 3 . 6 and y d = 8 . 4 2 8 5 2 3 0 0 2 .
Solving for:
⎩ ⎪ ⎨ ⎪ ⎧ x c 2 + y c 2 = ( c + 1 4 ) 2 ( x c − 3 5 ) 2 + y c 2 = ( c + 2 1 ) 2 ( x c − x d ) 2 + ( y c − y d ) 2 = ( c + 2 ) 2
We get x c = 1 2 . 2 9 5 6 9 4 0 4 , y c = 1 8 . 8 6 8 8 9 5 3 8 and c = 8 . 5 2 1 5 2 9 8 0 7
Solving for:
⎩ ⎪ ⎨ ⎪ ⎧ x e 2 + y e 2 = ( R − 1 4 ) 2 ( x e − 3 5 ) 2 + y c 2 = ( R − 2 1 ) 2 ( x e − x c ) 2 + ( y e − y c ) 2 = ( R − c ) 2
We get R = 3 6 . 7 5 7 7 8 7 6 9
⇒ ⌊ 1 0 0 ( c + R ) ⌋ = ⌊ 1 0 0 ( 8 . 5 2 1 5 2 9 8 0 7 + 3 6 . 7 5 7 7 8 7 6 9 ) ⌋ = 4 5 2 7
We can use Descartes' circle theorem here to solve for the 2 radii.
I haven't used Descartes' circle theorem.. :3
Descartes Circle Theorem applies to 4 mutually tangent circles and is as follows:
( k 1 + k 2 + k 3 + k 4 ) 2 = 2 ( k 1 2 + k 2 2 + k 3 2 + k 4 2 )
Where k n is ± r n 1 where r n is the radius of the nth circle. The " ± " signifies that it is positive if the circle is externally tangent to the other circles and is negative if it is internally tangent to the other circles.
This can be rewritten as follows:
k 4 = k 1 + k 2 + k 3 ± 2 k 1 k 2 + k 1 k 3 + k 2 k 3
Then we can use circles A, B, and D for circles 1, 2, and 3 in the equation. Circle C becomes circle 4 in the equation and we can plug in as follows:
c 1 = 2 1 1 + 1 4 1 + 2 1 ± 2 2 1 1 1 4 1 + 2 1 1 2 1 + 1 4 1 2 1
There are two circles that are mutually tangent to circles A, B, and D. The first is circle C, which is the radius we're trying to find, and the second is a very small circle that can be drawn inside the gap between circles A, B, and D. Since we want to find the larger radius, we want the smaller curvature so ± becomes − . This gives us:
c = 1 3 − 1 1 1 2 1 ≈ 8 . 5 2 1 5
Now we do the same to find R, this time using circles A, B, and C for circles 1, 2, and 3 in the equation and circle E as circle 4 in the equation:
R 1 = 2 1 1 + 1 4 1 + c 1 ± 2 2 1 1 1 4 1 + 2 1 1 c 1 + 1 4 1 c 1
Since circle E is externally tangent to the other circles, the curvature should be negative and ± becomes − again. Then take the absolute value R to give us:
R = 4 1 1 1 − 4 1 4 2 ≈ 3 6 . 7 5 7 8
Finally ⌊ 1 0 0 ( c + R ) ⌋ is 4 5 2 7 .