Crazy Cosine Calculus!
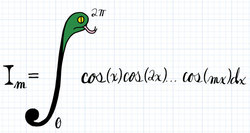 Let
I
m
=
∫
0
2
π
cos
(
x
)
cos
(
2
x
)
…
cos
(
m
x
)
d
x
. What is the sum of all integers
1
0
0
≤
m
≤
1
1
0
such that
I
m
=
0
?
Let
I
m
=
∫
0
2
π
cos
(
x
)
cos
(
2
x
)
…
cos
(
m
x
)
d
x
. What is the sum of all integers
1
0
0
≤
m
≤
1
1
0
such that
I
m
=
0
?
The answer is 522.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I think you only showed that I_m is zero if m=4n+1 or 4n+2, but you did not prove that it is not zero otherwise. Or do I miss something here?
Nicely done!
If we use the identity c o s z = 2 e i z + e − i z , we can rewrite the integral as ∫ 0 2 π k = 1 ∏ m 2 e i k x + e − i k x d x = 2 m 1 a k = ± 1 ∑ ∫ 0 2 π e i ( a 1 + 2 a 2 + 3 a 3 + ⋯ + m a m ) x d x .
Furthermore, note that ∫ 0 2 π e i n x d x = 2 π if n = 0 , otherwise it is equal to 0 as n ranges in the integers. Recall that e i x = cos x + i sin x , so the real and imaginary parts of the graph of e i n x from 0 to 2 π is the cosine and sine graph, respectively, repeated n times, so the integral is zero. Unless n = 0 , in which case it is the horizontal line y = 1 , which has an area of 2 π .
Since our integral ranges over all 2 m m-tuples of ( a 1 , a 2 , … , a m ) with a k = ± 1 , it suffices to show that, for a given m , there exists such a sequence { a k } such that a 1 + 2 a 2 + ⋯ + m a m = 0 .
So, 0 = a 1 + 2 a 2 + ⋯ + m a m ≡ 1 + 2 + ⋯ + m = 2 m ( m + 1 ) ( m o d 2 ) , thus 4 ∣ m ( m + 1 ) and m ≡ 0 , 3 ( m o d 4 ) .
Consider m ≡ 0 ( m o d 4 ) . Then we find a solution in ( 1 − 2 − 3 + 4 ) + ( 5 − 6 − 7 + 8 ) + ⋯ + ( ( m − 3 ) − ( m − 2 ) − ( m − 1 ) + m )
Consider m ≡ 3 ( m o d 4 ) . Then we find a solution in ( 1 + 2 − 3 ) + ( 4 − 5 − 6 + 7 ) + ⋯ + ( ( m − 3 ) − ( m − 2 ) − ( m − 1 ) + m ) .
Thus, I m = 0 iff m ≡ 0 , 3 ( m o d 4 ) . This gives the solution set of { 1 0 0 , 1 0 3 , 1 0 4 , 1 0 7 , 1 0 8 } , with sum 5 2 2 . ■
Great problem!
Log in to reply
yes indeed, nice problem. i sorta forgot about the cos(z) = (e^(iz) + e^(-iz))/2 =P
but the problem beatifully combines number theory, calculus and complex numbers along with clever thinking and a couple tricks here and there =)
but im guessing this is one of the "easier" putnam problems? (or is it one of the harder ones? @Michael Tong) <-- this reminds me, Brilliant should add a tagging system similar to facebook and forums so that one can tag another as "@Username".
Log in to reply
This was from the first year of putnam, but it was near the end (recall that they give 12 questions; 6 in each batch, I believe this was the 2nd to last problem so that means it's on the harder side)
Looks like your wishes came true.
I used the same argument but without Euler's formula:
(*) cos ( x ) cos ( y ) ⇒ f m ( x ) = 2 1 ( cos ( x − y ) + cos ( x + y ) , : = k = 1 ∏ m cos ( k x ) ( ∗ ) = 2 m − 1 1 a k = ± 1 ∑ cos ( ( 1 a 1 + … + m a m ) x ) x , y ∈ R
The rest works exactly the same!
This can be solved using the property
f ( 2 a − x ) = f ( x ) ⇒ ∫ 0 2 a f ( x ) d x = 2 ∫ 0 a f ( x ) d x
Let f ( x ) = cos ( x ) cos ( 2 x ) … cos ( m x ) ⇒ f ( 2 π − x ) = cos ( 2 π − x ) cos ( 4 π − 2 x ) … cos ( 2 m π − m x ) ⇒ f ( 2 π − x ) = cos ( x ) cos ( 2 x ) … cos ( m x )
(Since cos ( 2 n π ± θ ) = cos ( θ ) where n is an integer )
⇒ f ( 2 π − x ) = f ( x )
Thus,
I m = 2 ∫ 0 π cos ( x ) cos ( 2 x ) … cos ( m x ) d x . . . ( i )
Now, we know that ∫ 0 a f ( x ) d x = ∫ 0 a f ( a − x ) d x
Therefore
I m = 2 ∫ 0 π cos ( π − x ) cos ( 2 π − 2 x ) … cos ( m π − m x ) d x
Thus I m = + 2 ∫ 0 π cos ( x ) cos ( 2 x ) … cos ( m x ) d x = I m
when m = 4 n + 3 or m = 4 n ; n ∈ I n t e g e r s
And
I m = − 2 ∫ 0 π cos ( x ) cos ( 2 x ) … cos ( m x ) d x = − I m ⇒ 2 I m = 0 ⇒ I m = 0
when m = 4 n + 1 or m = 4 n + 2 ; n ∈ I n t e g e r s
Thus, I m = 0 for
m = 1 0 0 , 1 0 3 , 1 0 4 , 1 0 7 , 1 0 8
Thus,
A n s w e r = 1 0 0 + 1 0 3 + 1 0 4 + 1 0 7 + 1 0 8 = 5 2 2