Crazy Generalisation!

Geometry Level 5

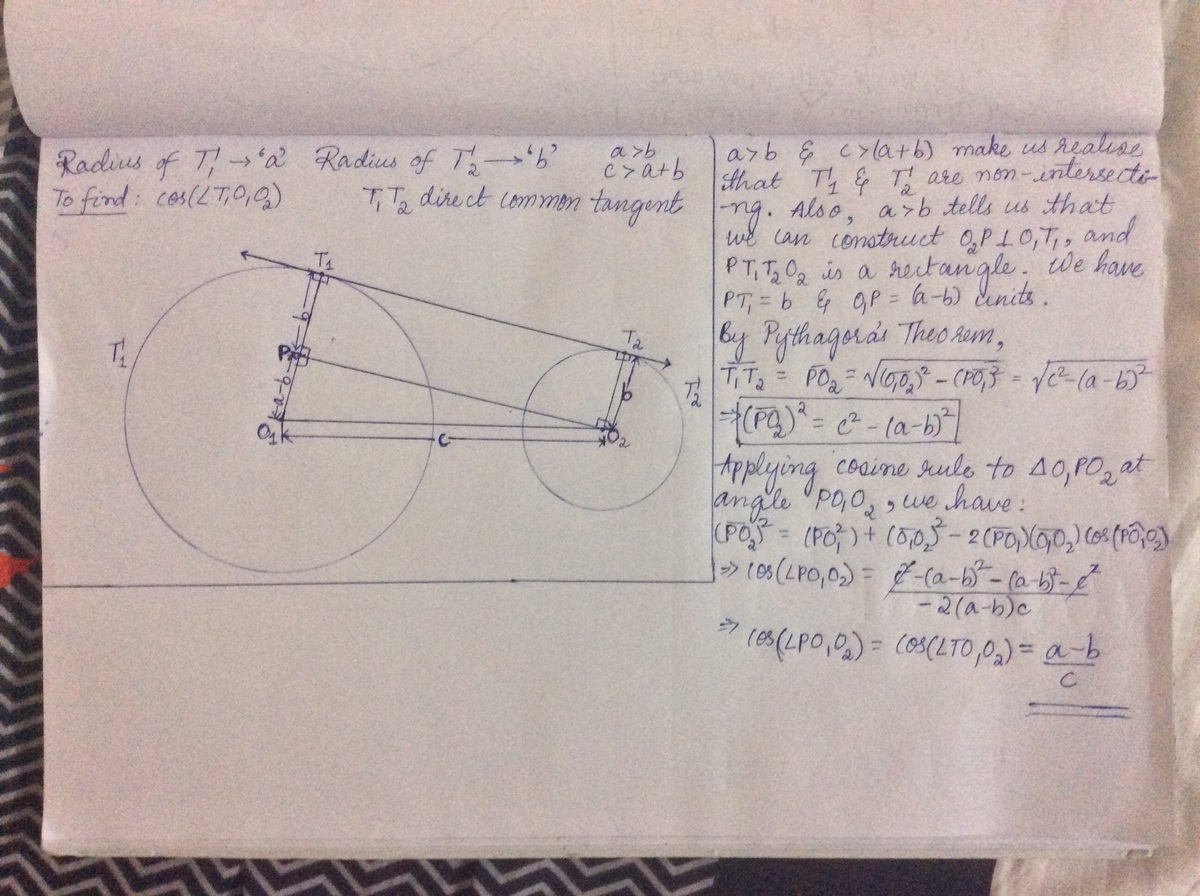
Consider two circles $\Gamma_{1}$ and $\Gamma_{2}$ with centres $O_{1}$ and $O_{2}$ in the Euclidean plane. Let $\Gamma_{1}$ and $\Gamma_{2}$ have radii $a$ and $b$ units respectively, $a > b > 0$ and $O_{1}O_{2}$ be $c$ units, with $c > (a+b)$ . Construct a direct common tangent $T_{1}T_{2}$ to these circles, with $T_{1}$ and $T_{2}$ on $\Gamma_{1}$ and $\Gamma_{2}$ respectively. Find $\cos(\angle T_{1}O_{1}O_{2})$ in terms of $a,b$ and $c$ .

Note: The direct common tangent has both circles lie on the same side of the line.

\dfrac{(a^{2}-b^{2})}{c}

\dfrac{(a-b)^{2}}{c^{2}}

\dfrac{(a-b)}{c}

\dfrac{(a^{2}-b^{2})}{c^{2}}

\dfrac{(a+b)}{c^{2}}

\dfrac{(a+b)}{c}

\dfrac{(a-b)^{2}}{c}

\dfrac{(a-b)}{c^{2}}

3 solutions

Niranjan Khanderia
Aug 22, 2015

$Let~~ T_2P~||~O_2O_1~cut~T_1O_1~at ~~P.\\ \Delta T_1PT_2~is ~a~rt\angle d~at~T_1,~~ T_1P=a-b,~~\angle\alpha=T_1O_1O_2.\\ \alpha=Cos^{-1}\dfrac{a-b} c.$
Just provided a diagram for what comments we have.

Venkata Karthik Bandaru
Aug 21, 2015

SOLUTION : Edit: As suggested by Sudeep Salgia sir, no need to apply cosine rule here. We directly have the relation in a right angled triangle $O_{1}PO_{2}$ .

Moderator note:

Good observation with the right triangle.

Sometimes, when the answer has a really simple form, you can think about alternative approaches that will get us to the answer. For example, can we find a right triangle with lengths of $a - b$ and $c$ ? If so, how does that relate to the given angle?

You don't even need to apply the cosine rule. It is a right angled triangle so the cosine can be computed directly and easily.

Sudeep Salgia - 5 years, 9 months ago

Oh lol, I am the best at over complicating solutions ! Thanks for identifying sir.

Venkata Karthik Bandaru - 5 years, 9 months ago

Thanks for sharing the quick approach!

Calvin Lin Staff - 5 years, 9 months ago

Good observation with the right triangle.

Calvin Lin Staff - 5 years, 9 months ago

I have done through Direct rt. angled triangle. The angle between the tangents is twice the angle found. In Engineering, this is the belt drive between two pulleys. Theoretically the two hanging portion of the belt are the tangents. It also apply to cross belts for internal tangents. For belt drive, c>>a+b.

We may note one more thing. For n circles having common direct tangents and tangential with two adjoining circles, (just touching the two adjoining circles) the radii are in GP. In Brilliant.org, there are several problems based on this.

Niranjan Khanderia - 5 years, 9 months ago

Wow ! Thanks for letting us know sir :).

Venkata Karthik Bandaru - 5 years, 9 months ago

Nibedan Mukherjee
Aug 22, 2015

very simple! take the difference of the two radii i.e (a-b) & since the hypotenuse of the triangle generated by joining the two centers of the circles O1 & O2 is given 'c', so simply cos(T1O1O2) = BASE/HYPOTENUSE = (a-b)/c

Correct, try to incorporate $\LaTeX$ .

Venkata Karthik Bandaru - 5 years, 9 months ago

We must not have options . Look in hustle I forgot to remove square of a-b and lost my points

Aakash Khandelwal - 5 years, 9 months ago

Crazy Generalisation!

3 solutions

Moderator note:

0 pending reports